
����Ŀ���ס��������̳���ͬһ����Ʒ��չ��������Թ������Ʒ�Ĺ˿������̳��Ľ�����������:
���̳�:�˿�ת����ͼ��ʾԲ�̣���ָ��ָ����Ӱ����(ͼ��������Ӱ���־�Ϊ���Σ���ÿ������Բ�ĽǾ�Ϊ![]() ���߽���Բ���)��Ϊ�н���
���߽���Բ���)��Ϊ�н���
���̳�:��װ��2������2�������2������ĺ�����һ��������1��(��Щ�����ɫ����ȫ��ͬ)�����Ǻ���ĸ�����![]() �����Ӻ�����һ��������2������������2����ͬ��ɫ����Ϊ�н�.
�����Ӻ�����һ��������2������������2����ͬ��ɫ����Ϊ�н�.

������ʵ��![]() ��ֵ��
��ֵ��
�������ʣ��������Ʒ�Ĺ˿����ļ��̳��н��Ŀ����Դ���˵������.
���𰸡�����![]() ;���˿��ڼ��̳��н��Ŀ����Դ�.
;���˿��ڼ��̳��н��Ŀ����Դ�.
���������������������������¼��ĸ��ʹ�ʽ,�������![]() ��ֵ��������˿�ȥ���̳�ת��Բ�̣�ָ��ָ����Ӱ����Ϊ�¼�
��ֵ��������˿�ȥ���̳�ת��Բ�̣�ָ��ָ����Ӱ����Ϊ�¼�![]() �����ü��θ�������˿�ȥ���̳��н��ĸ��ʣ���˿�ȥ���̳�һ������������ͬ��ɫ����Ϊ�¼�
�����ü��θ�������˿�ȥ���̳��н��ĸ��ʣ���˿�ȥ���̳�һ������������ͬ��ɫ����Ϊ�¼�![]() �����õȿ����¼����ʼ��㹫ʽ����˿�ȥ���̳��н��ĸ��ʣ��ɴ�������˿��ڼ��̳��н��Ŀ����Դ�
�����õȿ����¼����ʼ��㹫ʽ����˿�ȥ���̳��н��ĸ��ʣ��ɴ�������˿��ڼ��̳��н��Ŀ����Դ�
�������������������¼��ĸ��ʹ�ʽ�� ![]() �����
�����![]() .
.
������˿�ȥ���̳�ת��Բ�̣�ָ��ָ����Ӱ����Ϊ�¼�![]() �������ȫ��������ɵ�����ΪԲ�̣�
�������ȫ��������ɵ�����ΪԲ�̣�
���Ϊ![]() ��
��![]() ΪԲ�̵İ뾶������Ӱ��������Ϊ
ΪԲ�̵İ뾶������Ӱ��������Ϊ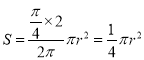 .
.
���ɼ��θ��ͣ��� .
.
��˿�ȥ���̳�һ������������ͬ��ɫ����Ϊ�¼�![]() ����2������Ϊ��1����2��2������Ϊ��1����2��2������Ϊ��1����2.
����2��������1����2��2��������1����2��2��������1����2.
��Ӻ�����һ��������2��һ�п��ܵĽ���У���1����2��������1����1��������1����2��������1����1��������1����2��������2����1��������2����2��������2����1��������2����2��������1����1��������1����2��������2����1��������2����2��������1����2���ȹ�15�֣�
������������2����ͬ��ɫ�����У���1����2��������1����2��������1����2���ȹ�3�֣�
���ɹŵ���ͣ���![]() .
.
��Ϊ![]() �����Թ˿��ڼ��̳��н��Ŀ����Դ�.
�����Թ˿��ڼ��̳��н��Ŀ����Դ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Sn����������{an}��ǰn��ͣ���Sn= ![]() an2+
an2+ ![]() an��
an�� ![]()
��1��������{an}��ͨ�ʽ��
��2����an=2nbn �� ������{bn}��ǰn��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ�⣺��֪����C1�� ![]() ����Ϊ������������C2��
����������������C2�� 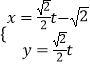 ��t��������
��t��������
��1��ָ��C1 �� C2����ʲô���ߣ���˵��C1��C2������ĸ�����
��2������C1 �� C2�ϸ���������궼ѹ��Ϊԭ����һ�룬�ֱ�õ�����C1�䣬C2�䣮д��C1�䣬C2��IJ������̣�C1����C2�乫����ĸ�����C��C2������ĸ����Ƿ���ͬ��˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]()
![]() ��
�� ![]() ������ԭ�㣬
������ԭ�㣬 ![]() �ֱ�Ϊ�����ҽ��㣬
�ֱ�Ϊ�����ҽ��㣬 ![]() ,
, ![]() ����Բ��һ�㣬
����Բ��һ�㣬 ![]() �����ֵΪ
�����ֵΪ![]()
��������Բ![]() �ķ���;
�ķ���;
������ֱ��![]() ����Բ
����Բ![]() ����
����![]() ���㣬��
���㣬��![]()
��i����֤�� ![]() Ϊ��ֵ;
Ϊ��ֵ;
��ii����![]() �����ȡֵ��Χ.
�����ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�õ�����y=sin��2x+ ![]() ����ͼ��ֻ�轫����y=sin2x��ͼ�� ��
����ͼ��ֻ�轫����y=sin2x��ͼ�� ��
A.����ƽ�� ![]() ���ȵ�λ
���ȵ�λ
B.����ƽ�� ![]() �����ȵ�λ
�����ȵ�λ
C.����ƽ�Ƹ� ![]() ���ȵ�λ
���ȵ�λ
D.����ƽ�� ![]() ���ȵ�λ
���ȵ�λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��У��2012��������������Գɼ��������ȡ100��ѧ���ı��Գɼ������ɼ����飬�õ���Ƶ�ʷֲ�������ͼ��ʾ��
��I���������Ƶ�ʷֲ����Т١���λ����Ӧ���ݣ����ڴ���ֽ���������Ƶ�ʷֲ�ֱ��ͼ��
������Ϊ����ѡ�γ��������ѧ������У�����ڱ��Գɼ��ߵĵ�3��4��5�����÷ֲ������ȡ6��ѧ������ڶ������ԣ����3��4��5��ÿ�����ȡ������ѧ������ڶ������ԣ�
����������2����ǰ���£�ѧУ������6��ѧ���������ȡ2��ѧ������A���ٵ����ԣ���4��������һ��ѧ��������A���Եĸ��ʣ�
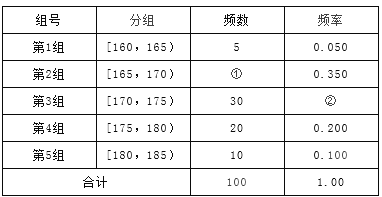
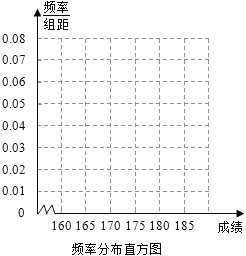
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �Ķ��κ���
�Ķ��κ���![]() ��
��
��1���輯��![]() ��
��![]() ,�ֱ�Ӽ���
,�ֱ�Ӽ���![]() �����ȡһ������Ϊ
�����ȡһ������Ϊ![]() ��
��![]() ,����
,����![]() ������
������![]() �����������ĸ��ʣ�
�����������ĸ��ʣ�
��2�����![]() ������
������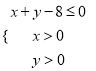 �ڵ������, ����
�ڵ������, ����![]() ������
������![]() �����������ĸ��ʣ�
�����������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֲ�Ʒÿ���ɱ�Ϊ6Ԫ,ÿ���ۼ�Ϊ![]() Ԫ(
Ԫ(![]() ),������
),������![]() ���,����֪
���,����֪![]() ��
��![]() ������,���ۼ�Ϊ10Ԫʱ,������Ϊ28���.
������,���ۼ�Ϊ10Ԫʱ,������Ϊ28���.
(1)������������![]() �����ۼ�
�����ۼ�![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
(2)���ۼ�Ϊ����ʱ,���������,��������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() ����γ���ÿ��γ����������ͺͱ��������ͺţ�ij�µIJ������±�(��λ����)�������÷ֲ�����ķ���������������Ľγ��г�ȡ50����������A��γ�10����
����γ���ÿ��γ����������ͺͱ��������ͺţ�ij�µIJ������±�(��λ����)�������÷ֲ�����ķ���������������Ľγ��г�ȡ50����������A��γ�10����
�γ� | �γ� | �γ� | |
������ | 100 | 150 |
|
���� | 300 | 450 | 600 |
(1)��![]() ��ֵ��
��ֵ��
(2)�÷ֲ�����ķ�����![]() ��γ��г�ȡһ������Ϊ5��������������������һ�����壬������ȡ
��γ��г�ȡһ������Ϊ5��������������������һ�����壬������ȡ
2������������1�������ͽγ��ĸ��ʣ�
(3)����������ķ�����![]() �������ͽγ��г�ȡ8������������ǵĵ÷����£�
�������ͽγ��г�ȡ8������������ǵĵ÷����£�![]() . ����8���γ��ĵ÷ֿ���һ�����壬������ȡһ�����������������ƽ����֮��ľ��� ֵ������
. ����8���γ��ĵ÷ֿ���һ�����壬������ȡһ�����������������ƽ����֮��ľ��� ֵ������![]() �ĸ��ʣ�
�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com