
分析 分△=0与△>0讨论,当△>0时,利用x1+x2=2,x1x2=a,x12-2x1+a=0,x22-2x2+a=0化简f(x1)f(x2)>0可得a(a2-3a+3)>0,从而解得.
解答 解:(1)当△=4-4a=0,即a=1时,
x1=x2=1,f(x1)f(x2)=$(-\frac{2}{3})^{2}$>0,符合题意;
(2)当△=4-4a>0,即a<1时,
x1+x2=2,x1x2=a,x12-2x1+a=0,x22-2x2+a=0;
∴f(x1)=$\frac{1}{3}$x13-x12+ax1-a
=$\frac{1}{3}$x1(2x1-a)-(2x1-a)+ax1-a
=$\frac{2}{3}$x12-$\frac{1}{3}$ax1-2x1+a+ax1-a
=$\frac{2}{3}$(2x1-a)-$\frac{1}{3}$ax1-2x1+ax1
=$\frac{2}{3}$(a-1)x1-$\frac{2}{3}$a,
同理,f(x2)=$\frac{2}{3}$(a-1)x2-$\frac{2}{3}$a,
∴f(x1)f(x2)=[$\frac{2}{3}$(a-1)x1-$\frac{2}{3}$a][$\frac{2}{3}$(a-1)x2-$\frac{2}{3}$a]
=$\frac{4}{9}$((a-1)2x1x2-a(a-1)(x1+x2)+a2)
=$\frac{4}{9}$(a(a-1)2-2a(a-1)+a2)>0,
即a(a2-3a+3)>0,
∴a>0,
又∵a<1,
∴0<a<1;
故实数a的取值范围为(0,1].
点评 本题考查了分类讨论的思想应用及方程的根与系数的关系应用.


科目:高中数学 来源: 题型:选择题
| A. | 关于点$({\frac{π}{2},1})$对称 | B. | 关于直线x=π对称 | C. | 关于点(π,0)对称 | D. | 关于y轴对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2≤m≤4 | B. | R | C. | 2<m<4 | D. | m>4或m<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
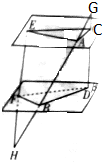 如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.
如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,1)∪(1,+∞) | D. | (-∞,0)∪(0,1)∪(1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com