
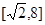 的两个函数
的两个函数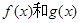 的解析式分别为
的解析式分别为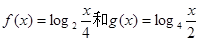
 ,
,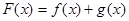 的值域;
的值域;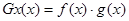 的值域.
的值域.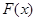 的值域为
的值域为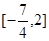 。(2)
。(2)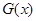 的值域为
的值域为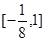

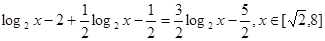 ,结合对数函数的性质得到最值。
,结合对数函数的性质得到最值。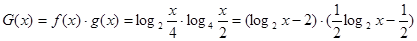
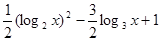 ,
,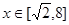 ,然后结合二次函数性质得到最值。
,然后结合二次函数性质得到最值。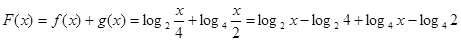
 ,-----2分
,-----2分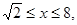 且
且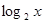 的值随着x的增大而增大,----------3分
的值随着x的增大而增大,----------3分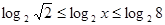 ,即
,即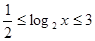 ,--------4分
,--------4分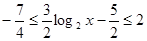 ,即
,即 ---------------5分
---------------5分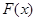 的值域为
的值域为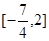 ---------------------6分
---------------------6分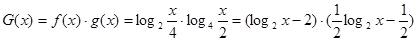
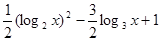 ,
,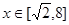 ,--------8分
,--------8分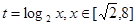 ,则有
,则有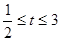 ,
,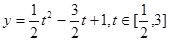 ,
,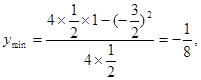
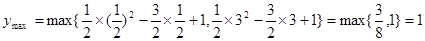 --------11分
--------11分 ,即
,即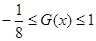 ,
,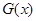 的值域为
的值域为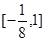 .-----------12分
.-----------12分

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源:不详 题型:填空题
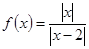 为偶函数; (2)函数
为偶函数; (2)函数 ;
;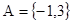 ,
,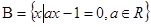 ,若
,若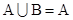 ,则实数
,则实数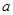 的取值集合为
的取值集合为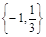 ; (4)集合
; (4)集合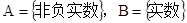 ,对应法则f:“求平方根”,则
,对应法则f:“求平方根”,则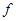 是A到B的映射;你认为正确命题的序号是 (把正确的序号都写上).
是A到B的映射;你认为正确命题的序号是 (把正确的序号都写上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com