
【题目】国庆节来临,某公园为了丰富广大人民群众的业余生活,特地以“我们都是中国人”为主题举行猜谜语竞赛.现有两类谜语:一类叫事物谜,就是我们常说的谜语;另一类叫文义谜,也就是我们常说的灯谜,共8道题,其中事物谜4道题,文义谜4道题,孙同学从中任取3道题解答.
(1)求孙同学至少取到2道文义谜题的概率;
(2)如果孙同学答对每道事物谜题的概率都是![]() ,答对每道文义谜题的概率都是
,答对每道文义谜题的概率都是![]() ,且各题答对与否相互独立,已知孙同学恰好选中2道事物谜题,1道文义谜题,用
,且各题答对与否相互独立,已知孙同学恰好选中2道事物谜题,1道文义谜题,用![]() 表示孙同学答对题的个数,求随机变量
表示孙同学答对题的个数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;(2)答案见解析,
;(2)答案见解析,![]() .
.
【解析】
(1)由题意可知孙同学至少取到2道文义谜题的有两种情况:一是孙同学取到2道文义谜题,另一种是孙同学取到3道文义谜题,这两种情况是互斥的,根据互斥事件概率的求法求解即可;
(2)由于孙同学从中任取3道题解答,用![]() 表示孙同学答对题的个数,所以
表示孙同学答对题的个数,所以![]() 可能的取值有0,1,2,3四种情况,分别求四种情况下的概率,即可得到分布列,进而可求出期望.
可能的取值有0,1,2,3四种情况,分别求四种情况下的概率,即可得到分布列,进而可求出期望.
解:(1)设“孙同学至少取到2道文义谜题”为事件![]() .
.
孙同学取到2道文义谜题共有![]() 种取法;
种取法;
孙同学取到3道文义谜题共有![]() 种取法,
种取法,
故![]() .
.
(2)易知![]() 的所有可能取值为0,1,2,3.
的所有可能取值为0,1,2,3.
则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
故随机变量![]() 的数学期望
的数学期望![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1
的值越接近于1
B.若正态分布![]() ,则
,则![]()
C.把某中学的高三年级560名学生编号:1到560,再从编号为1到10的10名学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
,![]() ,
,![]() ,…的学生,这样的抽样方法是分层抽样
,…的学生,这样的抽样方法是分层抽样
D.若一组数据0,![]() ,3,4的平均数是2,则该组数据的方差是
,3,4的平均数是2,则该组数据的方差是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]()
![]() .经过点
.经过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(其中点
两点(其中点![]() 在
在![]() 轴上方),
轴上方),![]() 的周长为
的周长为![]() .
.
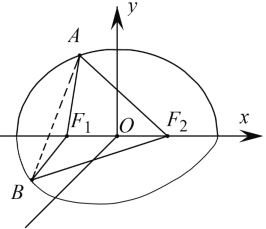
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,把平面![]() 沿
沿![]() 轴折起来,使
轴折起来,使![]() 轴正半轴和
轴正半轴和![]() 轴确定的半平面,与
轴确定的半平面,与![]() 轴负半轴和
轴负半轴和![]() 轴所确定的半平面互相垂直,若折叠后
轴所确定的半平面互相垂直,若折叠后![]() 的周长为
的周长为![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,点E在AB上,AE=2EB=2,且DE⊥AB.以DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.
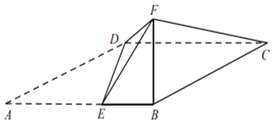
(1)求证:平面BFC⊥平面BCDE;
(2)若直线DF与平面BCDE所成角的正切值为![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
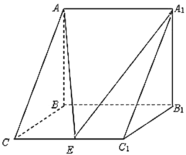
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,过曲线![]() 外的一点
外的一点![]() (其中
(其中![]() ,
,![]() 为锐角)作平行于
为锐角)作平行于![]() 的直线
的直线![]() 与曲线分别交于
与曲线分别交于![]() .
.
(Ⅰ) 写出曲线![]() 和直线
和直线![]() 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为![]() 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com