
(本题满分14分)在一个特定时段内,以点![]() 为中心的7海里以内海域被设为警戒水域.点
为中心的7海里以内海域被设为警戒水域.点![]() 正北55海里处有一个雷达观测站
正北55海里处有一个雷达观测站![]() .某时刻测得一艘匀速直线行驶的船只位于点
.某时刻测得一艘匀速直线行驶的船只位于点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() ,经过40分钟又测得该船已行驶到点
,经过40分钟又测得该船已行驶到点![]() 北偏东
北偏东![]() +
+![]() (其中
(其中
sin![]() =
=![]() ,
,![]() )且与点
)且与点![]() 相距
相距![]() 海里的位置C.
海里的位置C.
(Ⅰ)求该船的行驶速度(单位:海里/小时);
(Ⅱ)该船不改变航行方向继续行驶,判断它是否会进入警戒水域;若进入请求出经过警戒水域的时间,并说明理由.

南安一中2010-2011学年高一年(下)期末考试数学试卷
解:(I)如图,AB=40![]() ,AC=10
,AC=10![]() ,
,![]()
由于![]() ,所以cos
,所以cos![]() =
=![]() …………………………2分
…………………………2分
由余弦定理得BC=![]() …………………………4分
…………………………4分
所以船的行驶速度为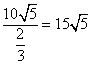 (海里/小时) …………………………6分
(海里/小时) …………………………6分
(II)解法一 如图所示,以A为原点建立平面直角坐标系,
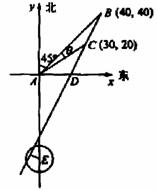 设点B、C的坐标分别是B(x1,y2), C(x1,y2),BC与x轴的交点为D.
设点B、C的坐标分别是B(x1,y2), C(x1,y2),BC与x轴的交点为D.
由题设有,x1=y1= ![]() AB=40,
AB=40,
x2=ACcos![]() ,
,
y2=ACsin![]()
所以过点B、C的直线l的斜率k=![]() ,直线l的方程为y=2x-40. …………………………9分
,直线l的方程为y=2x-40. …………………………9分
又点E(0,-55)到直线l的距离d=![]()
故该船会进入警戒水域. …………………………12分
进入警戒水域所行驶的路程为![]() 海里 …………………………13分
海里 …………………………13分
![]() 小时,所以经过警戒水域的时间为
小时,所以经过警戒水域的时间为![]() 小时. …………………………14分
小时. …………………………14分
解法二: 如图所示,设直线AE与BC的延长线相交于点Q.
在△ABC中,由余弦定理得,
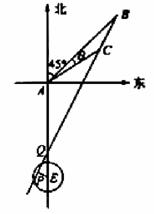
![]() =
=![]() =
=![]() . …………………8分
. …………………8分
从而![]()
在![]() 中,由正弦定理得,
中,由正弦定理得,
AQ=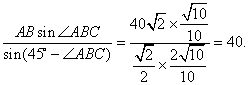 ……………………10分
……………………10分
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.
过点E作EP ![]() BC于点P,则EP为点E到直线BC的距离.
BC于点P,则EP为点E到直线BC的距离.![]()
在Rt![]() 中,
中,
PE=QE·sin![]() =
=![]() ………12分
………12分
故该船会进入警戒水域.
进入警戒水域所行驶的路程为![]() 海里 …………………………13分
海里 …………………………13分
![]() 小时,所以经过警戒水域的时间为
小时,所以经过警戒水域的时间为![]() 小时. …………………………14分
小时. …………………………14分


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
(本题满分14分)
在平面直角坐标系中,已知向量![]() (
(![]() ),
),![]() ,动点
,动点![]() 的轨迹为T.
的轨迹为T.
(1)求轨迹T的方程,并说明该方程表示的曲线的形状;
(2)当![]() 时,已知
时,已知![]() 、
、![]() ,试探究是否存在这样的点
,试探究是否存在这样的点![]() :
: ![]() 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积![]() ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省黄冈中学高二上学期期中考试理科数学试卷(带解析) 题型:解答题
(本题满分14分)在平面直角坐标系 中,已知圆
中,已知圆 ,
,
圆 .
.
(Ⅰ)若过点 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)圆 是以1为半径,圆心在圆
是以1为半径,圆心在圆 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆 上任意一点
上任意一点 分别作圆
分别作圆 的两条切线
的两条切线 ,切点为
,切点为 ,求
,求 的取值范围 ;
的取值范围 ;
(Ⅲ)若动圆 同时平分圆
同时平分圆 的周长、圆
的周长、圆 的周长,如图所示,则动圆
的周长,如图所示,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省杭州市求是高复高三11月月考文科数学 题型:解答题
(本题满分14分)
在 中,角
中,角 、
、 、
、 所对应的边分别为
所对应的边分别为 、
、 、
、 ,且满足
,且满足
(1)若 ,求实数
,求实数 的值。
的值。
(2)若 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省中山市高三上学期期末考试文科数学 题型:解答题
.(本题满分14分)
在棱长为 的正方体
的正方体 中,
中,
 是线段
是线段 的中点,底面ABCD的中心是F.
的中点,底面ABCD的中心是F.
(1) 求证: ^
^ ;
;
(2) 求证: ∥平面
∥平面 ;
;
(3) 求三棱锥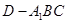 的体积。
的体积。

查看答案和解析>>
科目:高中数学 来源:海南省10-11学年高一下学期期末考试数学(1班) 题型:解答题
(本题满分14分)在直角坐标系xOy中,椭圆C1: 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 .
.
(Ⅰ)求C1的方程;
(Ⅱ)平面上的点N满足 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
· =0,求直线l的方程.
=0,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com