
【题目】定义在![]() 上的奇函数
上的奇函数![]() 有最小正周期
有最小正周期![]() ,且
,且![]() 时,
时,![]() .
.
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)判断![]() 在
在![]() 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当![]() 为何值时,关于方程
为何值时,关于方程![]() 在
在![]() 上有实数解?
上有实数解?
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(1).公路上![]() 、
、![]() 两镇相距5公里,
两镇相距5公里,![]() 、
、![]() 往外各有两条叉路成
往外各有两条叉路成![]() 形状,计划在每条叉路上各建一加油站,要求每个站到
形状,计划在每条叉路上各建一加油站,要求每个站到![]() 、
、![]() 镇及其他站(沿公路进过
镇及其他站(沿公路进过![]() 、
、![]() 镇)距离互不相同,且距离均为整数公里,最长不超过15公里,此计划能否实现?
镇)距离互不相同,且距离均为整数公里,最长不超过15公里,此计划能否实现?
(2).若![]() 、
、![]() 向外各有3条叉路,欲建六个加油站,依然要求站与镇,站与站之间距离互不相同且为整数公路,最长者不超过28公里,能否实现?为什么?
向外各有3条叉路,欲建六个加油站,依然要求站与镇,站与站之间距离互不相同且为整数公路,最长者不超过28公里,能否实现?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A. B. C的对边分别为a,b,c,己知![]() =b(c-asinC)。
=b(c-asinC)。
(1)求角A的大小;
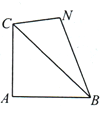
(2)设b=c,N是△ABC所在平面上一点,且与A点分别位于直线BC的两侧,如图,若BN=4,CN=2,求四边形ABNC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() .
.
(1)试讨论f(x)的单调性;
(2)若函数![]() 有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且
有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且![]() 的最大值是e2,求x1x3的最大值.
的最大值是e2,求x1x3的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“2019曹娥江国际马拉松”在上虞举行,现要选派5名志愿者服务于![]() 四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
四个不同的运动员救助点,每个救助点至少分配1人,若志愿者甲要求不到A救助点,则不同的分派方案有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
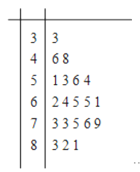
(1)根据以上资料完成下面的![]() 列联表,若据此数据算得
列联表,若据此数据算得![]() ,则在犯错的概率不超过
,则在犯错的概率不超过![]() 的前提下,你是否认为“满意与否”与“性别”有关?
的前提下,你是否认为“满意与否”与“性别”有关?
不满意 | 满意 | 合计 | |
男 | 4 | 7 | |
女 | |||
合计 |
附:
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
(2)估计用户对该公司的产品“满意”的概率;
(3)该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com