
【题目】已知函数![]() .
.
(1)若函数![]() 在区间
在区间![]() 内是单调递增函数,求实数a的取值范围;
内是单调递增函数,求实数a的取值范围;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .(注:
.(注:![]() 为自然对数的底数)
为自然对数的底数)
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)函数![]() 在区间
在区间![]() 上是单调递增函数,
上是单调递增函数,![]() ,化为:
,化为:![]() ,
,![]() .利用二次函数的单调性即可得出.
.利用二次函数的单调性即可得出.
(2)![]() 在区间
在区间![]() 上有两个不相等的实数根,方程
上有两个不相等的实数根,方程![]() 在区间
在区间![]() 上有两个不相等的实数根.令
上有两个不相等的实数根.令![]() ,利用根的分布可得
,利用根的分布可得![]() 的范围,再利用根与系数关系可得:
的范围,再利用根与系数关系可得:![]() ,得
,得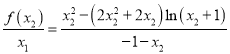 ,令
,令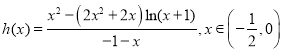 .利用导数研究其单调性极值与最值即可得出.
.利用导数研究其单调性极值与最值即可得出.
(1)解:∵函数![]() 在区间
在区间![]() 上是单调递增函数,
上是单调递增函数,
∴![]() ,化为:
,化为:![]() ,
,![]() ,
,
令![]() ,则
,则![]() 时取等号.
时取等号.
![]() .
.
∴实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)证明:![]() 在区间
在区间![]() 上有两个不相等的实数根,
上有两个不相等的实数根,
即方程![]() 在区间
在区间![]() 上有两个不相等的实数根,
上有两个不相等的实数根,
记![]() ,则
,则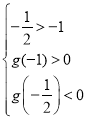 ,解得
,解得![]() ,
,
![]() ,
,
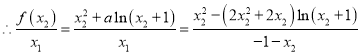 ,
,
令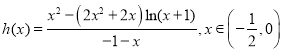 ,
,
![]() ,
,
记![]() ,
,
![]() ,
,
令![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,
,
因此函数![]() 存在唯一零点
存在唯一零点![]() ,使得
,使得![]() ,
,
当![]() ;当
;当![]() 时,
时,![]() ,
,
而![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
而![]() ,
,
![]() ,
,
![]() ,
,
∴函数![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,
可得:![]() ,
,
即![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,下图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每卦有三根线组成(“![]() ”表示一根阳线,“
”表示一根阳线,“![]() ”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率__________.
”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列.中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现了杨辉三角.在欧洲,帕斯卡在1654年也发现了这一规律,所以这个表又叫做帕斯卡三角形.杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合.
第0行 | 1 |
第1行 | 1 1 |
第2行 | 1 2 1 |
第3行 | 1 3 3 1 |
第4行 | 1 4 6 4 1 |
第5行 | 1 5 10 10 5 1 |
第6行 | 1 6 15 20 15 6 1 |
(1)记杨辉三角的前n行所有数之和为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)在杨辉三角中是否存在某一行,且该行中三个相邻的数之比为![]() ?若存在,试求出是第几行;若不存在,请说明理由;
?若存在,试求出是第几行;若不存在,请说明理由;
(3)已知n,r为正整数,且![]() .求证:任何四个相邻的组合数
.求证:任何四个相邻的组合数![]() ,
,![]() ,
,![]() ,
,![]() 不能构成等差数列.
不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
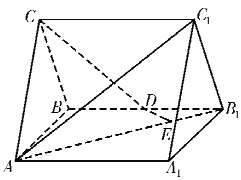
(I)若![]() 为
为![]() 上的一点,且
上的一点,且![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的条件下,设异面直线![]() 与
与![]() 所成的角为45°,求直线
所成的角为45°,求直线![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数在![]() 和
和![]() 处有两个极值点,其中
处有两个极值点,其中![]() ,
,![]() .
.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)若![]() (e为自然对数的底数),求
(e为自然对数的底数),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
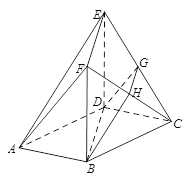
【题目】(本小题满分12分)如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的的菱形,
的的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数a满足1<a≤2,设函数f (x)=![]() x3-
x3-![]() x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com