
(08年衡阳八中理)( 13分) 已知点H(0,3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足![]() ,
,![]() .
.
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程;
(2)过定点A(a,b)的直线与曲线C相交于两点S、R,求证:曲线C在S、R两点处的切线的交点B恒在一条直线上.
解析:(1)解:设P(a,0),Q(0,b)
则:![]() ∴
∴![]() …………1分
…………1分
设M(x,y)∵![]()
∴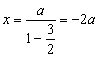
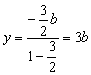 …………4分
…………4分
∴点M的轨迹曲线C的方程是![]() (x≠0) . …………6分
(x≠0) . …………6分
(2)解法一:设A(a,b),![]() ,
,![]() (x1≠x2)
(x1≠x2)
则:直线SR的方程为: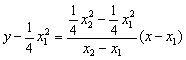 ,即4y = (x1+x2)x-x1x2
,即4y = (x1+x2)x-x1x2
∵A点在SR上,∴4b=(x1+x2)a-x1x2 ① …………8分
对![]() 求导得:y′=
求导得:y′=![]() x
x
∴抛物线上S、R处的切线方程为:
![]() 即4
即4![]() ②
②
![]() 即4
即4![]() ③ …………11分
③ …………11分
联立②③,并解之得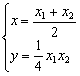 ,代入①得:ax-2y-2b=0
,代入①得:ax-2y-2b=0
故B点恒在直线ax-2y-2b=0上. …………13分
解法二:设A(a,b)
当过点A的直线斜率不存在时l与抛物线有且仅有一个公共点,与题意不符,可设直线SR的方程为y-b=k(x-a)
与![]() 联立消去y得:x2-4kx+4ak-4b=0 …………8分
联立消去y得:x2-4kx+4ak-4b=0 …………8分
设![]() ,
,![]() (x1≠x2)
(x1≠x2)
则由韦达定理:![]() …………9分
…………9分
又过S、R点的切线方程分别为:![]() ,
,![]() …………11分
…………11分
故有 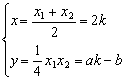 (k为参数)
(k为参数)
消去k,得:ax-2y-2b=0
故B点恒在直线ax-2y-2b=0上. …………13分


科目:高中数学 来源: 题型:
(08年衡阳八中理) (12分) 在△ABC中,A,B,C是三角形的三内角,a,b,c是三内角对应的三边,已知![]()
(1)求角A大小;
(2)若![]() ,判断△ABC的形状.
,判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年衡阳八中理)(12分)如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.
(1)求二面角A-PB-D的大小,
(2)在线段PB上是否存在一点E,使PC⊥平面ADE?若存在,确定E点的位置,若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年衡阳八中理) (12分) 甲、乙两名射击运动员,甲射击一次命中10环的概率为![]() ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=![]() ,
,![]() 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.
(1)求s的值及![]() 的分布列,
的分布列,
(2)求![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com