
【题目】已知函数,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 有
有![]() 个不同的零点,求实数
个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时
时![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() 在
在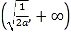 上单调递增,
上单调递增,![]() 在
在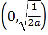 上单调递减.(2)
上单调递减.(2)![]()
【解析】
(1)分![]() 两种情况讨论导数的符号后可得函数的单调区间.
两种情况讨论导数的符号后可得函数的单调区间.
(2)根据(1)可知![]() 且
且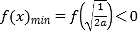 ,后者可得实数
,后者可得实数![]() 的取值范围为
的取值范围为![]() ,再根据
,再根据![]() ,
,![]() 结合零点存在定理可知当
结合零点存在定理可知当![]() 时函数确有两个不同的零点.
时函数确有两个不同的零点.
(1)解:因为![]() ,
,
①当![]() 时,总有
时,总有![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
②当![]() 时,令
时,令![]() ,解得
,解得![]() .
.
故![]() 时,
时,![]() ,所以
,所以![]() 在
在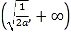 上单调递增.
上单调递增.
同理![]() 时,有
时,有![]() ,所以
,所以![]() 在
在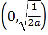 上单调递减.
上单调递减.
(2)由(1)知当![]() 时,
时,![]() 单调递减,
单调递减,
所以函数![]() 至多有一个零点,不符合已知条件,
至多有一个零点,不符合已知条件,
由(1)知当![]() 时,
时,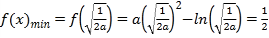
![]() ,
,
所以![]() 当时,解得
当时,解得![]() ,从而
,从而![]() .
.
又![]() 时,有
时,有![]() ,因为
,因为![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 为增函数,故
为增函数,故![]() ,
,
所以![]() ,根据零点存在定理可知:
,根据零点存在定理可知:
![]() 在
在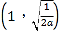 内有一个零点,在
内有一个零点,在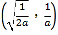 内有一个零点,
内有一个零点,
故当函数![]() 有
有![]() 个零点时,
个零点时,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,下表是在某单位调查后得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:
①从赞同“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行陈述发言,求事件“男士和女士各至少有
人进行陈述发言,求事件“男士和女士各至少有![]() 人发言”的概率;
人发言”的概率;
②从反对“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行座谈,设选出的
人进行座谈,设选出的![]() 人中女士人数为
人中女士人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
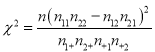
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年高考总成绩由语数外三门统考科目和物理、化学等六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为![]() 、
、![]() 、
、![]() 、
、![]() 共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到
共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 八个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩
八个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩![]() 大致服从正态分布
大致服从正态分布![]() .
.
(1)求该市化学原始成绩在区间![]() 的人数;
的人数;
(2)以各等级人数所占比例作为各分数区间发生的概率,按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间![]() 的人数,求
的人数,求![]() .
.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了鼓励运动提高所有用户的身体素质,特推出一款运动计步数的软件,所有用户都可以通过每天累计的步数瓜分红包,大大增加了用户走步的积极性,所以该软件深受广大用户的欢迎.该公司为了研究“日平均走步数和性别是否有关”,统计了2019年1月份所有用户的日平均步数,规定日平均步数不少于8000的为“运动达人”,步数在8000以下的为“非运动达人”,采用按性别分层抽样的方式抽取了100个用户,得到如下列联表:
运动达人 | 非运动达人 | 总计 | |
男 | 35 | 60 | |
女 | 26 | ||
总计 | 100 |
(1)(i)将![]() 列联表补充完整;
列联表补充完整;
(ii)据此列联表判断,能否有![]() 的把握认为“日平均走步数和性别是否有关”?
的把握认为“日平均走步数和性别是否有关”?
(2)从样本中的运动达人中抽取7人参加“幸运抽奖”活动,通过抽奖共产生2位幸运用户,求这2位幸运用户恰好男用户和女用户各一位的概率.
附:
|
|
|
|
|
|
|
|
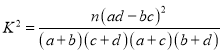
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一劳动节放假,某商场进行一次大型抽奖活动.在一个抽奖盒中放有红、橙、黄、绿、蓝、紫的小球各2个,分别对应1分、2分、3分、4分、5分、6分.从袋中任取3个小球,按3个小球中最大得分的8倍计分,计分在20分到35分之间即为中奖.每个小球被取出的可能性都相等,用![]() 表示取出的3个小球中最大得分,求:
表示取出的3个小球中最大得分,求:
(1)取出的3个小球颜色互不相同的概率;
(2)随机变量![]() 的概率分布和数学期望;
的概率分布和数学期望;
(3)求某人抽奖一次,中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 这
这![]() 个自然数随机地排列在
个自然数随机地排列在![]() 的正方形方格内,对于同一行或同一列中的任意两个数,计算较大数与较小数的商,得到
的正方形方格内,对于同一行或同一列中的任意两个数,计算较大数与较小数的商,得到![]() 个分数.把最小的分数称之为这种排列的“特征值”.试求特征值的最大值.
个分数.把最小的分数称之为这种排列的“特征值”.试求特征值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“回文数”是指从左到右与从右到左读都一样的正整数,如22,121,3553等.显然2位“回文数”共9个:11,22,33,…,99.现从9个不同2位“回文数”中任取1个乘以4,其结果记为X;从9个不同2位“回文数”中任取2个相加,其结果记为Y.
(1)求X为“回文数”的概率;
(2)设随机变量![]() 表示X,Y两数中“回文数”的个数,求
表示X,Y两数中“回文数”的个数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C![]() (t∈R,t≠0)为圆心的圆与x轴交于点O和点A,与y轴交于点O和点B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O和点A,与y轴交于点O和点B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y=-2x+4与圆C交于点M,N,若OM=ON,求圆C的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com