
【题目】如图,在直角坐标 ![]() 中,设椭圆
中,设椭圆 ![]()
![]() 的左右两个焦点分别为
的左右两个焦点分别为 ![]() ,过右焦点
,过右焦点 ![]() 且与
且与 ![]() 轴垂直的直线
轴垂直的直线 ![]() 与椭圆
与椭圆 ![]() 相交,其中一个交点为
相交,其中一个交点为 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
【答案】
(1)解:由椭圆定义可知 ![]()
由题意 ![]() ,
, ![]() .
.
又由Rt△ ![]() 可知
可知 ![]() ,
, ![]() ,
, ![]() ,
,
又 ![]() ,得
,得 ![]()
![]() 椭圆
椭圆 ![]() 的方程为
的方程为 ![]()
(2)已知 ![]() 经过点
经过点 ![]() 且斜率为
且斜率为 ![]() 直线
直线 ![]() 与椭圆
与椭圆 ![]() 有两个不同的
有两个不同的 ![]() 和
和 ![]() 交点,请问是否存在常数
交点,请问是否存在常数 ![]() ,使得向量
,使得向量 ![]() 与
与 ![]() 共线?如果存在,求出
共线?如果存在,求出 ![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
解:设直线 ![]() 的方程为
的方程为 ![]() ,
,
代入椭圆方程,得 ![]() .
.
整理,得 ![]() ①
①
因为直线 ![]() 与椭圆
与椭圆 ![]() 有两个不同的交点
有两个不同的交点 ![]() 和
和 ![]() 等价于
等价于 ![]() ,
,
解得 ![]() .
.
设 ![]() ,则
,则 ![]() =
= ![]() ,
,
由①得 ![]() ②
②
又 ![]() ③
③
因为 ![]() , 所以
, 所以 ![]() .
.
所以 ![]() 与
与 ![]() 共线等价于
共线等价于 ![]() .
.
将②③代入上式,解得 ![]() .
.
因为 ![]()
所以不存在常数 ![]() ,使得向量
,使得向量 ![]() 与
与 ![]() 共线
共线
【解析】(1)根据题目中所给的条件的特点,由椭圆定义可知|MF1|+|MF2|=2a,由题意|MF2|=1,由Rr△MF1F2可知b的值,则椭圆C的方程可求;
(2)利用向量共线的条件建立等式,再根据韦达定理,由此能求出不存在这样的常数k满足条件.解题时要认真审题,注意向量共线的条件的合理运用.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
【题目】已知圆C的方程:x2+y2﹣2x﹣4y+m=0,其中m<5.
(1)若圆C与直线l:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(2)在(1)条件下,是否存在直线l:x﹣2y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围,若不存在,说明理由.
,若存在,求出c的范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共 ![]() 个,生产一个卫兵需
个,生产一个卫兵需 ![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需 ![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需 ![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过 ![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润 ![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润 ![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润 ![]() 元.
元.
(1)用每天生产的卫兵个数 ![]() 与骑兵个数
与骑兵个数 ![]() 表示每天的利润
表示每天的利润 ![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面α过正方体ABCD﹣A1B1C1D1的面对角线 ![]() ,且平面α⊥平面C1BD,平面α∩平面ADD1A1=AS,则∠A1AS的正切值为( )
,且平面α⊥平面C1BD,平面α∩平面ADD1A1=AS,则∠A1AS的正切值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD.
(1)求证:EF∥平面PAD;
(2)若EF⊥PC,求证:平面PAB⊥平面PCD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“石头、剪刀、布”,又称“猜丁壳”,是一种流传多年的猜拳游戏,起源于中国,然后传到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近代逐渐风靡世界.其游戏规则是:出拳之前双方齐喊口令,然后在话音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”、“剪刀”胜“布”、而“布”又胜过“石头”.若所出的拳相同,则为和局.小千和大年两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,则小千和大年比赛至第四局小千胜出的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥C﹣ABDE中,DB⊥平面ABC,AE∥DB,△ABC是边长为2的等边三角形,AE=1,M为AB的中点. 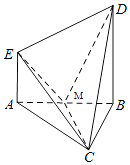
(1)求证:CM⊥EM;
(2)若直线DM与平面ABC所成角的正切值为2,求二面角B﹣CD﹣E的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com