
【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】
(1)解:设等差数列{an}的公差为d,
∵a1+1,a2+1,a4+1成等比数列,∴ ![]() =(a1+1)(a4+1),
=(a1+1)(a4+1),
又S3=﹣15,∴ ![]() =﹣15,∴a2=﹣5.
=﹣15,∴a2=﹣5.
∴(﹣5+1)2=(﹣5﹣d+1)(﹣5+2d+1),解得d=0或d=﹣2.
d=0时,公比为1,舍去.
∴d=﹣2.
∴an=a2﹣2(n﹣2)=﹣5﹣2(n﹣2)=﹣2n﹣1
(2)解:由(1)可得:Sn= ![]() =﹣n2﹣2n.
=﹣n2﹣2n.
∴bn= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]()
![]() ,
,
∴数列{bn}的前n项和Tn= ![]()
![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]()
=﹣ ![]()
![]()
=﹣ ![]() +
+ ![]()
【解析】(1)设等差数列{an}的公差为d,根据a1+1,a2+1,a4+1成等比数列,可得 ![]() =(a1+1)(a4+1),又S3=﹣15,可得
=(a1+1)(a4+1),又S3=﹣15,可得 ![]() =3a2=﹣15,解得a2 , 进而得到d.即可得出an . (2)由(1)可得:Sn=﹣n2﹣2n.可得bn=
=3a2=﹣15,解得a2 , 进而得到d.即可得出an . (2)由(1)可得:Sn=﹣n2﹣2n.可得bn= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]()
![]() ,利用“裂项求和”即可得出.
,利用“裂项求和”即可得出.
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系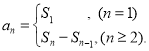 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的奇函数,且当x≥0时,f(x)=x2﹣(a+4)x+a.
(1)求实数a的值及f(x)的解析式;
(2)求使得f(x)=x+6成立的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC= ![]() ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( ) 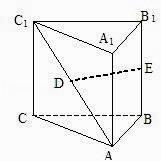
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: ①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′﹣DEF的体积最大值为 ![]() a3;
a3;
④动点A′在平面ABC上的射影在线段AF上;
⑤二面角A′﹣DE﹣F大小的范围是[0, ![]() ].
].
其中正确的命题是(写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求a,b,c的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)的定义域为(﹣a,0)∪(0,a)(0<a<1),其图象上任意一点P(x,y)满足x2+y2=1,则给出以下四个命题:①函数y=f(x)一定是偶函数;②函数y=f(x)可能是奇函数;③函数y=f(x)在(0,a)上单调递增④若函数y=f(x)是偶函数,则其值域为(a2 , 1)其中正确的命题个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在x轴上,离心率为 ![]() ,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A,B. (Ⅰ)求椭圆的方程;
,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A,B. (Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)若直线l不过点M,求证:直线MA、MB与x轴围成一个等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1 . (Ⅰ)求数列{bn}的通项公式;
(Ⅱ)令cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com