
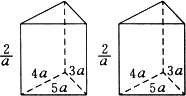
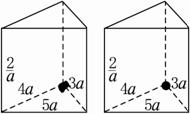
如图,有两个相同的直三棱柱,高为![]() ,底面三角形的三边长分别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则a的取值范围是________.
,底面三角形的三边长分别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则a的取值范围是________.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:黄冈中学 高二数学(下册)、考试卷5 简单几何体同步测试卷(二) 题型:044
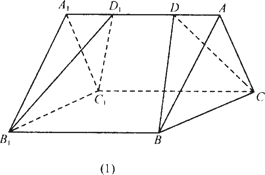
从2004年开始,某市政府准备在市区实施“景观工程”,以现有平顶的民用多层住宅进行“平改坡”,计划将平顶房屋改为尖顶,并铺上彩色瓦片,现对某幢房屋有如下两种改造方案:
方案一:坡顶如图(1)所示,为顶面是等腰三角形的直三棱柱,尖顶屋脊![]() 与房屋长度
与房屋长度![]() 等长,有两个坡面需铺上瓦片.
等长,有两个坡面需铺上瓦片.
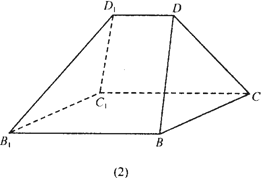
方案二:坡顶如图(2)所示,为由(1)削去两端相同的两个三棱锥而得,尖顶屋脊![]() 比房屋长度
比房屋长度![]() 要短,有四个坡面需铺上瓦片.
要短,有四个坡面需铺上瓦片.
若房屋长度![]() ,宽BC=2b,屋脊高为h,试问哪种方案尖顶铺设的瓦片比较省?说明理由.
,宽BC=2b,屋脊高为h,试问哪种方案尖顶铺设的瓦片比较省?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com