
【题目】如图①,有一个等腰直角三角板![]() 垂直于平面
垂直于平面![]() ,有一条长为7的细线,其两端分别位于
,有一条长为7的细线,其两端分别位于![]() 处,现用铅笔拉紧细线,在平面
处,现用铅笔拉紧细线,在平面![]() 上移动.
上移动.
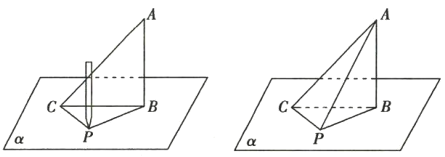
图① 图②
(1)图②中的![]() 的长为多少时,
的长为多少时,![]() 平面
平面![]() ?并给出证明.
?并给出证明.
(2)在(1)的情形下,求三棱锥![]() 的高.
的高.
【答案】(1)当![]() 时,
时,![]() 平面
平面![]() ,证明见解析;(2)
,证明见解析;(2)![]() .
.
【解析】
(1)若使得![]() 平面
平面![]() ,则需三角形
,则需三角形![]() 为直角三角形且
为直角三角形且![]() ,当
,当![]() 时,根据线面线面垂直的判定定理,证明即可.
时,根据线面线面垂直的判定定理,证明即可.
(2)方法一,过点![]() 作
作![]() 于点
于点![]() ,由(1)可知,
,由(1)可知,![]() ,则
,则![]() 平面
平面![]() ,即
,即![]() 为三棱锥
为三棱锥![]() 的高,在
的高,在![]() 中计算
中计算![]() ,再根据
,再根据![]() ,求解即可. 方法二,设三棱锥
,求解即可. 方法二,设三棱锥![]() 的高为
的高为![]() ,根据
,根据![]() ,求解即可.
,求解即可.
(1)当![]() 时,
时,![]() 平面
平面![]() .证明如下:
.证明如下:
若![]() ,则
,则![]()
因为![]() ,所以
,所以![]()
所以三角形![]() 为直角三角形,且
为直角三角形,且![]() .
.
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]()
所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
所以![]() 平面
平面![]() .
.
(2)方法一 如图,过点![]() 作
作![]() 于点
于点![]() .
.

由(1)知![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 为三棱锥
为三棱锥![]() 的高.
的高.
由于![]() 平面
平面![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() .即三棱锥
.即三棱锥![]() 的高为
的高为![]() .
.
方法二 由(1),知![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() .
.
又![]() ,
,
所以![]() ,即
,即![]() .
.
设三棱锥![]() 的高为
的高为![]() ,则
,则![]() .
.
又![]() ,
,
且![]() ,所以
,所以![]() ,即
,即![]() .
.
所以三棱锥![]() 的高为
的高为![]() .
.


科目:高中数学 来源: 题型:
【题目】某城市的华为手机专卖店对该市市民使用华为手机的情况进行调查.在使用华为手机的用户中,随机抽取100名,按年龄(单位:岁)进行统计的频率分布直方图如图:

(1)根据频率分布直方图,分别求出样本的平均数(同一组数据用该区间的中点值作代表)和中位数的估计值(均精确到个位);
(2)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加华为手机宣传活动,再从这20人中年龄在![]() 和
和![]() 的人群里,随机选取2人各赠送一部华为手机,求这2名市民年龄都在
的人群里,随机选取2人各赠送一部华为手机,求这2名市民年龄都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断![]() 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)若![]() ,试判断函数
,试判断函数![]() 的单调性,并用定义法证明;
的单调性,并用定义法证明;
(3)若已知![]() ,且函数
,且函数![]() 在区间[1,+∞)上的最小值为-2,求实数m的值.
在区间[1,+∞)上的最小值为-2,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院有内科医生8名,外科医生6名,现选派4名参加抗击新冠肺炎疫情医疗队,其中
(1)甲、乙两人至少有一人参加,有多少种选法?
(2)队中至少有一名内科医生和一名外科医生,有几种选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在其定义域内存在单调递减区间.
在其定义域内存在单调递减区间.
(1)求f(x)的单调递减区间;
(2)设函数![]() ,(e是自然对数的底数).是否存在实数a,使g(x)在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
,(e是自然对数的底数).是否存在实数a,使g(x)在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有10所学校,每所都选派若干名男生和若干名女生举行跳棋比赛,同一学校的选手不比赛,不同学校的选手不论男女在两人之间都要进行一场比赛. 在两个男生或两个女生之间的比赛总局数与男生和女生之间的比赛总局数与男生和女生之间的比赛总局数至多相差1,而男生的总人数和女生的总人数也至多相差1. 求证:至少有7所学校选派的男生和女生人数相同.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知n为给定的正整数,t为给定的实数,设(t+x)n=a0+a1x+a2x2+…+anxn.
(1)当n=8时.
①若t=1,求a0+a2+a4+a6+a8的值;
②若t=![]() ,求数列{an}中的最大值;
,求数列{an}中的最大值;
(2)若t=![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com