
【题目】已知函数f(x)=log ![]()
![]() 的图象关于原点对称,其中a为常数.
的图象关于原点对称,其中a为常数.
(1)求a的值;
(2)当x∈(1,+∞)时,f(x)+log ![]() (x+1)<m恒成立,求实数m的取值范围;
(x+1)<m恒成立,求实数m的取值范围;
(3)若关于x的方程f(x)=log ![]() (x+k)在[2,3]上有解,求k的取值范围.
(x+k)在[2,3]上有解,求k的取值范围.
【答案】
(1)
解:∵函数f(x)的图象关于原点对称,
∴函数f(x)为奇函数,
∴f(﹣x)=﹣f(x),
即log ![]()
![]() =﹣log
=﹣log ![]()
![]() = log
= log ![]()
![]() ,
,
解得:a=﹣1或a=1(舍)
(2)
解:f(x)+ log ![]() (x﹣1)= log
(x﹣1)= log ![]()
![]() + log
+ log ![]() (x﹣1)= log
(x﹣1)= log ![]() (1+x),
(1+x),
x>1时,log ![]() (1+x)<﹣1,
(1+x)<﹣1,
∵x∈(1,+∞)时,f(x)+ log ![]() (x﹣1)<m恒成立,
(x﹣1)<m恒成立,
∴m≥﹣1;
(3)
解:由(1)得:f(x)= log ![]() (x+k),
(x+k),
即log ![]()
![]() = log
= log ![]() (x+k),
(x+k),
即 ![]() =x+k,即k=
=x+k,即k= ![]() ﹣x+1在[2,3]上有解,
﹣x+1在[2,3]上有解,
g(x)= ![]() ﹣x+1在[2,3]上递减,
﹣x+1在[2,3]上递减,
g(x)的值域是[﹣1,1],
∴k∈[﹣1,1]
【解析】(1)根据函数的奇偶性,求出a的值即可;(2)求出f(x)+ log ![]() (x﹣1)= log
(x﹣1)= log ![]() (1+x),根据函数的单调性求出m的范围即可;(3)问题转化为k=
(1+x),根据函数的单调性求出m的范围即可;(3)问题转化为k= ![]() ﹣x+1在[2,3]上有解,即g(x)=
﹣x+1在[2,3]上有解,即g(x)= ![]() ﹣x+1在[2,3]上递减,根据函数的单调性求出g(x)的值域,从而求出k的范围即可.
﹣x+1在[2,3]上递减,根据函数的单调性求出g(x)的值域,从而求出k的范围即可.


科目:高中数学 来源: 题型:
【题目】已知圆C的方程:x2+y2﹣2x﹣4y+m=0,其中m<5.
(1)若圆C与直线l:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(2)在(1)条件下,是否存在直线l:x﹣2y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围,若不存在,说明理由.
,若存在,求出c的范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A是函数y=lg(6+5x﹣x2)的定义域,集合B是不等式x2﹣2x+1﹣a2≥0(a>0)的解集.p:x∈A,q:x∈B.
(1)若A∩B=,求a的取值范围;
(2)若¬p是q的充分不必要条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40﹣t(0≤t≤30且t∈N). 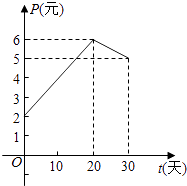
(1)根据提供的图象,求出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)用y(万元)表示该股票日交易额(日交易额=日交易量×每股的交易价格),写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x﹣2ay+a2﹣24=0(a∈R)的圆心在直线2x﹣y=0上.
(1)求实数a的值;
(2)求圆C与直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R)相交弦长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com