
【题目】已知实数a、b满足a2+b2-ab=3.
(1)求a-b的取值范围;
(2)若ab>0,求证:![]() .
.
【答案】(1)﹣2≤a﹣b≤2;(2)证明见解析.
【解析】
(1)由已知得a2+b2=3+ab≥2|ab|.
①当ab≥0时,3+ab≥2ab,解得ab≤3,即0≤ab≤3;
②当ab<0时,3+ab≥﹣2ab,解得 ab≥﹣1,即﹣1≤ab<0,
得0≤3﹣ab≤4,即0≤(a﹣b)2≤4,即﹣2≤a﹣b≤2;
(2)由(1)知0<ab≤3,可得![]() ,
,
利用配方法即可容易证明.
(1)因为a2+b2﹣ab=3,所以a2+b2=3+ab≥2|ab|.
①当ab≥0时,3+ab≥2ab,解得ab≤3,即0≤ab≤3;
②当ab<0时,3+ab≥﹣2ab,解得 ab≥﹣1,即﹣1≤ab<0,
所以﹣1≤ab≤3,则0≤3﹣ab≤4,
而(a﹣b)2=a2+b2﹣2ab=3+ab﹣2ab=3﹣ab,
所以0≤(a﹣b)2≤4,即﹣2≤a﹣b≤2;
(2)由(1)知0<ab≤3,
因为![]()
![]()
当且仅当ab=2时取等号,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 (t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程及弦AB的长;
(2)动点P在圆C上(不与A,B重合),试求△ABP的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近五年来某草场羊只数量与草场植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 | 1 | 2 | 3 | 4 | 5 |
羊只数量(万只) | 1.4 | 0.9 | 0.75 | 0.6 | 0.3 |
草地植被指数 | 1.1 | 4.3 | 15.6 | 31.3 | 49.7 |

根据表及图得到以下判断:①羊只数量与草场植被指数成减函数关系;②若利用这五组数据得到的两变量间的相关系数为![]() ,去掉第一年数据后得到的相关系数为
,去掉第一年数据后得到的相关系数为![]() ,则
,则![]() ;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|2x+2|,g(x)=|x+2|﹣|x﹣2a|+a.
(1)求不等式f(x)>4的解集;
(2)对x1∈R,x2∈R,使得f(x1)≥g(x2)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节期间,新型冠状病毒(2019﹣nCoV)疫情牵动每一个中国人的心,危难时刻全国人民众志成城.共克时艰,为疫区助力.我国S省Q市共100家商家及个人为缓解湖北省抗疫消毒物资压力,募捐价值百万的物资对口输送湖北省H市.
(1)现对100家商家抽取5家,其中2家来自A地,3家来自B地,从选中的这5家中,选出3家进行调研.求选出3家中1家来自A地,2家来自B地的概率.
(2)该市一商家考虑增加先进生产技术投入,该商家欲预测先进生产技术投入为49千元的月产增量.现用以往的先进技术投入xi(千元)与月产增量yi(千件)(i=1,2,3,…,8)的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且:
的附近,且:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,
,其中,![]() ,
,![]() ,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
附:对于一组数据(u1,v1)(u2,v2),其回归直线v=α+βu的斜率和截距的最小二乘法估计分别为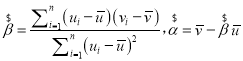
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节期间,新型冠状病毒(2019﹣nCoV)疫情牵动每一个中国人的心,危难时刻全国人民众志成城.共克时艰,为疫区助力.我国S省Q市共100家商家及个人为缓解湖北省抗疫消毒物资压力,募捐价值百万的物资对口输送湖北省H市.
(1)现对100家商家抽取5家,其中2家来自A地,3家来自B地,从选中的这5家中,选出3家进行调研.求选出3家中1家来自A地,2家来自B地的概率.
(2)该市一商家考虑增加先进生产技术投入,该商家欲预测先进生产技术投入为49千元的月产增量.现用以往的先进技术投入xi(千元)与月产增量yi(千件)(i=1,2,3,…,8)的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且:
的附近,且:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,
,其中,![]() ,
,![]() ,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
附:对于一组数据(u1,v1)(u2,v2),其回归直线v=α+βu的斜率和截距的最小二乘法估计分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行元旦促销回馈活动,凡购物满1000元,即可参与抽奖活动,抽奖规则如下:在一个不透明的口袋中装有编号为1、2、3、4、5的5个完全相同的小球,顾客每次从口袋中摸出一个小球,共摸三次(每次摸出的小球均不放回口袋),编号依次作为一个三位数的个位、十位、百位,若三位数是奇数,则奖励50元,若三位数是偶数,则奖励![]() 元(
元(![]() 为三位数的百位上的数字,如三位数为234,则奖励
为三位数的百位上的数字,如三位数为234,则奖励![]() 元).
元).
(1)求抽奖者在一次抽奖中所得三位数是奇数的概率;
(2)求抽奖者在一次抽奖中获奖金额![]() 的概率分布与期望
的概率分布与期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的普通方程为:
的普通方程为:![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,正方形
,正方形![]() 的顶点都在
的顶点都在![]() 上,且
上,且![]() 逆时针依次排列,点
逆时针依次排列,点![]() 的极坐标为
的极坐标为![]()
(1)写出曲线![]() 的参数方程,及点
的参数方程,及点![]() 的直角坐标;
的直角坐标;
(2)设![]() 为椭圆
为椭圆![]() 上的任意一点,求:
上的任意一点,求:![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com