
分析 (1)利用对数式的运算性质和运算法则即可求解.
(2)利用同角三角函数基本关系式即可得解cosα的值,由诱导公式化简所求即可求值.
解答 解:(1)原式=${log_6}4+{6^{{{log}_6}\sqrt{3}}}•{6^{-1}}+{log_6}{(\frac{1}{3})^{-2}}={log_6}36+\sqrt{3}•\frac{1}{6}=2+\frac{{\sqrt{3}}}{6}$(5分)
(2)原式=$\frac{-tanα•(-cosα)}{-cosα•sinα}=\frac{-1}{cosα}$,(2分)
∵tanα=2>0,∴α在第一或第三象限,
又∵sinα+cosα<0,
∴$cosα=-\frac{1}{{\sqrt{5}}}$,
故原式=$\sqrt{5}$(3分)
点评 本题主要考查了指数式和对数式的运算,同角三角函数基本关系式,诱导公式的应用,解题时要注意运算法则和运算性质的合理运用,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若事件A发生的概率为P(A),则0≤P(A)≤1 | |
| B. | 系统抽样是不放回抽样,每个个体被抽到的可能性相等 | |
| C. | 线性回归直线$\hat y=\hat bx+\hat a$必过点$(\overline x,\overline y)$ | |
| D. | 对于任意两个事件A和B,都有P(A∪B)=P(A)+P(B) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
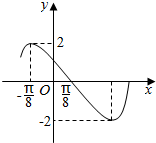 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )| A. | y=2sin(2x-$\frac{π}{4}$) | B. | y=2sin(2x-$\frac{π}{4}$)或y=2sin(2x+$\frac{3π}{4}$) | ||
| C. | y=2sin(2x+$\frac{3π}{4}$) | D. | y=2sin(2x-$\frac{3π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com