【题目】若函数
只有一个极值点，则k的取值范围为
A.
B.
C.
D.
【答案】B
【解析】
利用函数求导函数 f′（x）＝ex（x﹣2）﹣kx2+2kx＝（x﹣2）（ex﹣kx），只有一个极值点时f′（x）＝0只有一个实数解，有ex﹣kx≥0，设新函数设u（x）＝ex，v（x）＝kx，等价转化数形结合法即可得出结论，
解：函数f（x）＝ex（x﹣3）﹣
kx3+kx2只有一个极值点，
f′（x）＝ex（x﹣2）﹣kx2+2kx＝（x﹣2）（ex﹣kx），
若函数f（x）＝ex（x﹣3）﹣kx3+kx2只有一个极值点，f′（x）＝0只有一个实数解，
则：ex﹣kx≥0，
从而得到：ex≥kx，
当k＝0 时，成立．
当k≠0时，设u（x）＝ex，v（x）＝kx
如图：
当两函数相切时，k＝e，此时得到k的最大值，但k＜0时不成立．
故k的取值范围为：（0，e]
综上：k的取值范围为：[0，e]
故选：B．
科目：高中数学 来源： 题型：
【题目】保护环境，防治环境污染越来越得到人们的重视，某企业在现有设备下每日生产总成本
（单位：万元）与日产量
（单位：吨）之间的函数关系式为
．现为了减少大气污染，该企业引进了除尘设备，每吨产品除尘费用为
万元，除尘后，当日产量
时，每日生产总成本
．
（1）求的值；
（2）若每吨产品出厂价为48万元，试求除尘后日产量为多少吨时，每吨产品的利润最大，最大利润为多少万元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在倡导低碳、节能减排政策的推动下，越来越多的消费者选择购买新能源汽车.某品牌新能源汽车的行驶里程x（万公里）与该里程内维修保养的总费用y（千元）的统计数据如下：
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0.8 | 1.8 | 3.3 | 4.5 | 4.7 | 6.8 |
（1）根据表中数据建立y关于x的回归方程为
.我们认为，若残差绝对值
，则该数据为可疑数据，请找出上表中的可疑数据；
（2）经过确认，数据采集有误，（1）中可疑数据的维修保养总费用应增加0.7千元.请重新利用线性回归模型拟合数据.（精确到0.01）
附：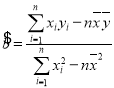
，
.
，
，
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系中，已知曲线
的参数方程为
（
为参数），以原点为极点，
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为：
，直线
的极坐标方程为
．
（Ⅰ）写出曲线的极坐标方程，并指出它是何种曲线；
（Ⅱ）设与曲线交于
，
两点，与曲线交于
，
两点，求四边形
面积的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆的焦点坐标是
，
，过点
垂直于长轴的直线交椭圆与
，
两点，且
.
（1）求椭圆方程：
（2）过坐标原点
做两条互相垂直的射线，与椭圆分别交于
，
两点，求证：点到直线
的距离为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（13分）设{an}是公比为正数的等比数列a1=2，a3=a2+4．
（Ⅰ）求{an}的通项公式；
（Ⅱ）设{bn}是首项为1，公差为2的等差数列，求数列{an+bn}的前n项和Sn．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P—ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，AB＝4，PA＝3，点A在PD上的射影为点G，点E在AB上，平面PEC⊥平面PDC.
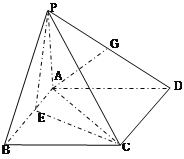
（1）求证：AG∥平面PEC；
（2）求AE的长；
（3）求二面角E—PC—A的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
