
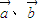 ,满足
,满足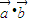 =0,则一定有
=0,则一定有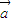 ⊥
⊥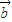 ;
;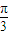 个单位,得到函数y=sin(2x-
个单位,得到函数y=sin(2x-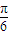 )的图象;
)的图象;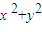 +Dx+Ey+F=0表示圆的充要条件是
+Dx+Ey+F=0表示圆的充要条件是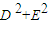 -4F≥0;
-4F≥0;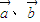 ,若
,若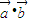 =0,则一定有
=0,则一定有 ⊥
⊥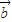 .
.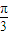 个单位,得到函数y=
个单位,得到函数y= ,再据诱导公式可进一步化出其表达式.
,再据诱导公式可进一步化出其表达式. +Dx+Ey+F=0配方化为
+Dx+Ey+F=0配方化为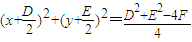 ,可以判断出④的真假.
,可以判断出④的真假.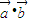 =0,则一定有
=0,则一定有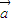 ⊥
⊥ .
.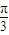 个单位,得到函数y=
个单位,得到函数y=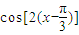 =
= =
=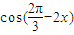 =
= =sin(2x-
=sin(2x-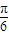 )
)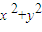 +Dx+Ey+F=0⇒
+Dx+Ey+F=0⇒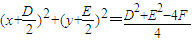 ,
, -4F>0时,方程
-4F>0时,方程 +Dx+Ey+F=0才表示一个圆,
+Dx+Ey+F=0才表示一个圆,

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| π |
| 6 |
| x | 2 |
| D | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| CD |
| a |
| b |
| b |
| c |
| a |
| c |
| AB |
| DC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省新乡市卫辉一中高三(下)3月月考数学试卷(理科)(解析版) 题型:解答题
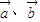 ,满足
,满足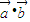 =0,则一定有
=0,则一定有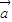 ⊥
⊥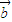 ;
;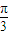 个单位,得到函数y=sin(2x-
个单位,得到函数y=sin(2x-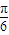 )的图象;
)的图象;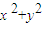 +Dx+Ey+F=0表示圆的充要条件是
+Dx+Ey+F=0表示圆的充要条件是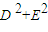 -4F≥0;
-4F≥0;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com