
分析 (1)由题意点P的轨迹是以A为焦点的抛物线,即可求得点P的轨迹方程;
(2)因为P在(1)中的抛物线上,设出P的坐标,求出PM的中点坐标,利用弦心距公式列式求出以PM为直径的圆与直线x=a的相交弦长,有弦长为定值可求得定值a的值.
解答 解:(1)∵$A(\frac{1}{4},0)$,动点P到点A的距离比到直线x=-$\frac{5}{4}$的距离少 1,
∴点P的轨迹是以A为焦点的抛物线,即点P的轨迹方程:y2=x(4分)
(2)由(1),点P的轨迹方程是y2=x;设P(y2,y),
∵M (4,0),则以PM为直径的圆的圆心即PM的中点T($\frac{{{y^2}+4}}{2}$,$\frac{y}{2}$),以PM为直径的圆与直线x=a的相交弦长:L=2$\sqrt{{{(\frac{{{y^2}+4}}{2}-4)}^2}+{{(\frac{y}{2}-0)}^2}-{{(\frac{{{y^2}+4}}{2}-a)}^2}}$=2$\sqrt{(a-4)({y^2}-a)+\frac{y^2}{4}}$(6分)
=2$\sqrt{(a-\frac{15}{4}){y^2}-a(a-4)}$(8分)
若a为常数,则对于任意实数y,L为定值的条件是a-$\frac{15}{4}$=0,即a=$\frac{15}{4}$时,L=$\frac{{\sqrt{15}}}{2}$(11分)
∴存在定直线x=$\frac{15}{4}$,以PM为直径的圆与直线x=$\frac{15}{4}$的相交弦长为定值$\frac{{\sqrt{15}}}{2}$.(12分)
点评 本题考查了抛物线方程的求法,考查了直线与圆的关系,训练了利用弦心距求弦长,是有一定难度题目.


科目:高中数学 来源: 题型:解答题
 某校高三年级在学期末进行的质量检测中,考生数学成绩情况如下表所示:
某校高三年级在学期末进行的质量检测中,考生数学成绩情况如下表所示:| 数学成绩 | [90,105) | [105,120) | [120,135) | [135,150] |
| 文科考生 | 57 | 40 | 24 | 6 |
| 理科考生 | 123 | x | y | z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | (1,5)∪(5,+∞) | D. | [1,5)∪(5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
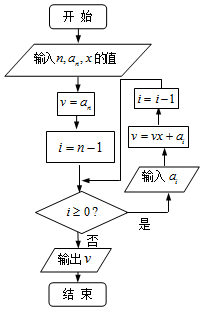 如图程序框图的算法思路,源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法,执行该程序框图,若输入的n,an,x分别为5,1,-2,且a4=5,a3=10,a2=10,a1=5,a0=1,则输出的v=( )
如图程序框图的算法思路,源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法,执行该程序框图,若输入的n,an,x分别为5,1,-2,且a4=5,a3=10,a2=10,a1=5,a0=1,则输出的v=( )| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2}\;\;,\;\;1})$ | B. | $({1\;\;,\;\;\sqrt{2}})$ | C. | $({\frac{3}{2}\;\;,\;\;\sqrt{3}})$ | D. | (2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com