
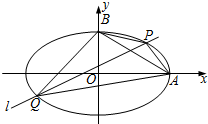
 ��֪ƽ��ֱ������ϵxOy�У���֪��Բ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0�����Ҷ�����϶���ֱ�ΪA��B����Բ��������Ϊ$\frac{\sqrt{3}}{2}$���ҹ��㣨1��$\frac{\sqrt{3}}{2}$����
��֪ƽ��ֱ������ϵxOy�У���֪��Բ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0�����Ҷ�����϶���ֱ�ΪA��B����Բ��������Ϊ$\frac{\sqrt{3}}{2}$���ҹ��㣨1��$\frac{\sqrt{3}}{2}$�������� ��1��ͨ�����㣨1��$\frac{\sqrt{3}}{2}$��������Բ���̣����������Ϊ$\frac{\sqrt{3}}{2}$���㼴�ý��ۣ�
��2��ͨ����1����֪A��2��0����B��0��1������ͨ����ֱ��AP�ķ���Ϊx=my+2��ֱ��BQ�ķ���Ϊx=-my+m���ֱ�����Բ���������������֪P��$\frac{8-2{m}^{2}}{4+{m}^{2}}$��-$\frac{4m}{4+{m}^{2}}$����Q��$\frac{8m}{4+{m}^{2}}$��$\frac{{m}^{2}-4}{4+{m}^{2}}$��������б�ʼ��㹫ʽ���㼴�ɣ���ͨ����1����ֱ֪��AB�ķ���Ϊx+2y-2=0��|AB|=$\sqrt{5}$��ͨ���ٿ�֪P��$\frac{8-2{m}^{2}}{4+{m}^{2}}$��-$\frac{4m}{4+{m}^{2}}$����Q��$\frac{8m}{4+{m}^{2}}$��$\frac{{m}^{2}-4}{4+{m}^{2}}$�������õ�P�ڵ�һ����֪-2��m��0���ֱ�������P��Q��ֱ��AB�ľ��룬���������������ʽ���㡢��ϻ�������ʽ���ý��ۣ�
��� ��1���⣺�����⣬$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{3}{4{b}^{2}}=1}\\{\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}=\frac{\sqrt{3}}{2}}\end{array}\right.$��
����ã�$\left\{\begin{array}{l}{4{b}^{2}+3{a}^{2}=4{a}^{2}{b}^{2}}\\{{a}^{2}=4{b}^{2}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{a}^{2}=4}\\{{b}^{2}=1}\end{array}\right.$��
����Բ�ı�����Ϊ��$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��2���ɣ�1����֪��A��2��0����B��0��1����ֱ��BQ��AP��б�ʾ������Ҳ�Ϊ0��
��֤������ֱ��AP�ķ���Ϊ��x=my+2����ֱ��BQ�ķ���Ϊ��x=-my+m��
����$\left\{\begin{array}{l}{x=my+2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$����ȥx�����ã���4+m2��y2+4my=0��
��P��$\frac{8-2{m}^{2}}{4+{m}^{2}}$��-$\frac{4m}{4+{m}^{2}}$����
����$\left\{\begin{array}{l}{x=-my+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$����ȥx�����ã���4+m2��y2-2m2y+m2-4=0��
��Q��$\frac{8m}{4+{m}^{2}}$��$\frac{{m}^{2}-4}{4+{m}^{2}}$����
��ֱ��l��б��Ϊ$\frac{\frac{{m}^{2}-4}{4+{m}^{2}}+\frac{4m}{4+{m}^{2}}}{\frac{8m}{4+{m}^{2}}-\frac{8-2{m}^{2}}{4+{m}^{2}}}$=$\frac{{m}^{2}+4m-4}{2{m}^{2}+8m-8}$=$\frac{1}{2}$��
�ڽ⣺�ɣ�1����ֱ֪��AB�ķ���Ϊ��x+2y-2=0��|AB|=$\sqrt{��2-0��^{2}+��0-1��^{2}}$=$\sqrt{5}$��
�ɢٿ�֪��P��$\frac{8-2{m}^{2}}{4+{m}^{2}}$��-$\frac{4m}{4+{m}^{2}}$����Q��$\frac{8m}{4+{m}^{2}}$��$\frac{{m}^{2}-4}{4+{m}^{2}}$����
�ߵ�P�ڵ�һ���ޣ�
��$\frac{1}{m}$��-$\frac{1}{2}$����-2��m��0��
���P��ֱ��AB�ľ���dP=$\frac{|\frac{8-2{m}^{2}}{4+{m}^{2}}-2��\frac{4m}{4+{m}^{2}}-2|}{\sqrt{{1}^{2}+{2}^{2}}}$=-$\frac{4{m}^{2}+8m}{\sqrt{5}��4+{m}^{2}��}$��
��Q��ֱ��AB�ľ���dQ=$\frac{|\frac{8m}{4+{m}^{2}}+2��\frac{{m}^{2}-4}{4+{m}^{2}}-2|}{\sqrt{{1}^{2}+{2}^{2}}}$=$\frac{16-8m}{\sqrt{5}��4+{m}^{2}��}$��
��$\frac{{S}_{1}}{{S}_{2}}$=$\frac{\frac{1}{2}|AB|{d}_{P}}{\frac{1}{2}|AB|{d}_{Q}}$=$\frac{{m}^{2}+2m}{2m-8}$=$\frac{1}{2}$[��m-4��+$\frac{24}{m-4}$+10]��
�ߣ�4-m��+$\frac{24}{4-m}$��2$\sqrt{��4-m��•\frac{24}{4-m}}$=4$\sqrt{6}$�����ҽ���4-m=$\frac{24}{4-m}$��m=4-2$\sqrt{6}$ʱȡ�Ⱥţ�
�ࣨm-4��+$\frac{24}{m-4}$��-4$\sqrt{6}$��
��$\frac{{S}_{1}}{{S}_{2}}$�����ֵΪ$\frac{1}{2}$��10-4$\sqrt{6}$��=5-2$\sqrt{6}$��
���� ������һ��ֱ����Բ���ߵ��ۺ��⣬�����������������ע����ⷽ���Ļ��ۣ������е��⣮


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��-1�� | B�� | ��4��7�� | C�� | ��-2��-1���ȣ�4��7�� | D�� | ∅ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ϲ����ѧ�γ� | ��ϲ����ѧ�γ� | �ܼ� | |
| �� | 37 | 85 | 122 |
| Ů | 35 | 143 | 178 |
| �ܼ� | 72 | 228 | 300 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com