
(本小题满分10分)
已知点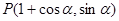 ,参数
,参数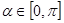 ,点Q在曲线C:
,点Q在曲线C: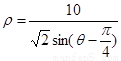 上.
上.
(1)求在直角坐标系中点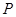 的轨迹方程和曲线C的方程;
的轨迹方程和曲线C的方程;
(2)求|PQ|的最小值.
(1)点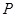 的轨迹是上半圆:
的轨迹是上半圆: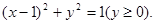 曲线C的直角坐标方程:
曲线C的直角坐标方程: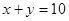 (2)
(2)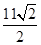 -1
-1
【解析】
试题分析:设点P的坐标为(x,y),则有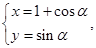 消去参数α,可得
消去参数α,可得 由于α∈[0,π],∴y≥0,故点P的轨迹是上半圆
由于α∈[0,π],∴y≥0,故点P的轨迹是上半圆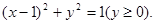 ∵曲线C:
∵曲线C: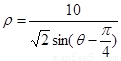 ,即
,即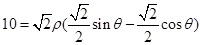 ,即 ρsinθ-ρcosθ=10,故曲线C的直角坐标方程:x-y+10=0.(2)如图所示:由题意可得点Q在直线x-y+10="0" 上,点P在半圆上,半圆的圆心C(1,0)到直线x-y+10=0的距离等于
,即 ρsinθ-ρcosθ=10,故曲线C的直角坐标方程:x-y+10=0.(2)如图所示:由题意可得点Q在直线x-y+10="0" 上,点P在半圆上,半圆的圆心C(1,0)到直线x-y+10=0的距离等于 .即|PQ|的最小值为
.即|PQ|的最小值为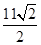 -1.
-1.
考点:本题考查了把参数方程、极坐标方程化为直角坐标方程的方法及直线与圆的位置关系
点评:对于参数方程与极坐标的考查,主要的就是考查参数方程和极坐标转化为普通方程的过程,有时需要注意参数和极坐标的角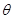 的范围.直线的极坐标方程的建立一般是通过直角三角形来处理
的范围.直线的极坐标方程的建立一般是通过直角三角形来处理


科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com