
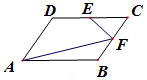
 如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$.
如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$. 分析 用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AE},\overrightarrow{EF}$,再计算数量积.
解答 解:∵四边形ABCD是边长为1菱形,E,F分别为DC、BC的中点,
∴$\overrightarrow{AF}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$,$\overrightarrow{EF}$=$\frac{1}{2}\overrightarrow{DB}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AD}$,$\overrightarrow{AB}•\overrightarrow{AD}$=1×1×cos60°=$\frac{1}{2}$,
∴$\overrightarrow{AF}•\overrightarrow{EF}$=($\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$)•($\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AD}$)=$\frac{1}{2}$${\overrightarrow{AB}}^{2}$-$\frac{1}{4}$$\overrightarrow{AD}$2-$\frac{1}{4}$$\overrightarrow{AB}•\overrightarrow{AD}$=$\frac{1}{2}-\frac{1}{4}$-$\frac{1}{8}$=$\frac{1}{8}$.
故答案为$\frac{1}{8}$.
点评 本题考查了平面向量的数量积运算,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
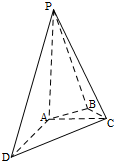 如图,在四棱锥P-ABCD中,PA丄平面ABCD,AB丄BC,∠BCA=45°,PA=AD=2,AC=1,DC=$\sqrt{5}$
如图,在四棱锥P-ABCD中,PA丄平面ABCD,AB丄BC,∠BCA=45°,PA=AD=2,AC=1,DC=$\sqrt{5}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | -150° | C. | 390° | D. | -390° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com