
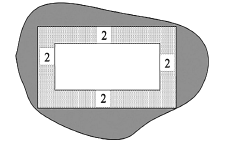
【题目】在城市旧城改造中,某小区为了升级居住环境,拟在小区的闲置地中规划一个面积为![]() 的矩形区域(如图所示),按规划要求:在矩形内的四周安排
的矩形区域(如图所示),按规划要求:在矩形内的四周安排![]() 宽的绿化,绿化造价为200元/
宽的绿化,绿化造价为200元/![]() ,中间区域地面硬化以方便后期放置各类健身器材,硬化造价为100元/
,中间区域地面硬化以方便后期放置各类健身器材,硬化造价为100元/![]() .设矩形的长为
.设矩形的长为![]() .
.
(1)设总造价![]() (元)表示为长度
(元)表示为长度![]() 的函数;
的函数;
(2)当![]() 取何值时,总造价最低,并求出最低总造价.
取何值时,总造价最低,并求出最低总造价.
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 和圆
和圆![]() .
.

(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为2
截得的弦长为2![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设![]() 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点![]() 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线![]() 和
和![]() ,且直线
,且直线![]() 被圆
被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题: 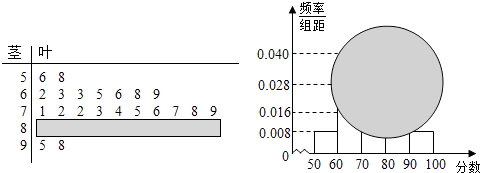
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)若规定:75(包含75分)分以上为良好,90分(包含90分)以上为优秀,要从分数在良好以上的试卷中任取两份分析学生失分情况,设在抽取的试卷中,分数为优秀的试卷份数为X,求X的概率分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com