
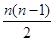 ×2]-49=-n2+20n-49 2分
×2]-49=-n2+20n-49 2分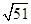 <n<10+
<n<10+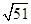 4分
4分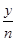 =-n-
=-n-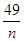 +20≤-2
+20≤-2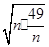 +20=6(万元) 7分
+20=6(万元) 7分

科目:高中数学 来源:不详 题型:解答题
 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
). 的最大值;
的最大值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。 的函数解析式
的函数解析式 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
, ,
, 的最小值为
的最小值为 .
. 的解析式;
的解析式; ,若
,若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;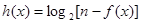 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.49 h | B.56 h | C.64 h | D.72 h |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com