
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间和函数
的单调区间和函数![]() 的最值;
的最值;
(2)已知关于![]() 的不等式
的不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案不唯一,见解析;(2)![]()
【解析】
(1)求导后,分![]() 和
和![]() 两种情况考虑
两种情况考虑![]() 的单调性;利用导数求
的单调性;利用导数求![]() 的极值即可;
的极值即可;
(2)![]() 对任意的
对任意的![]() 恒成立,等价于
恒成立,等价于![]() 对任意的
对任意的![]() 恒成立,设
恒成立,设![]() ,利用导数研究
,利用导数研究![]() 的单调性以及最值,从而可得到结论.
的单调性以及最值,从而可得到结论.
(1)因为![]() ,∴
,∴![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,![]() 在区间
在区间![]() 上单调递增.
上单调递增.
当![]() ,即
,即![]() 时,令
时,令![]() ,则
,则![]() 或
或![]() ,
,![]() 单调递增;令
单调递增;令![]() ,则
,则![]() ,
,![]() 单调递减.
单调递减.
综上,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ;
;
因为![]() ,(
,(![]() )
)
所以![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,所以
单调递减,所以![]() ,无最大值.
,无最大值.
(2)![]() 对任意的
对任意的![]() 恒成立,
恒成立,
即![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() ,
,![]() ,则
,则![]() .
.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() 在区间
在区间![]() 上单调递减.所以
上单调递减.所以![]() ,符合题意.
,符合题意.
当![]() 时,令
时,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]()
由(1)知![]() ,即
,即![]() 在
在![]() 上恒成立,不符合题意.
上恒成立,不符合题意.
综上,实数![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 的平行线,与直线
的平行线,与直线![]() 相交于点
相交于点![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,二面角
上运动时,二面角![]() 能否等于
能否等于![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,圆
,圆![]() ,点
,点![]() 为圆
为圆![]() 上动点,线段
上动点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,记
,记![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 与
与![]() 作平行直线
作平行直线![]() 和
和![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 、
、![]() 和点
和点![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中开设大学先修课程已有两年,两年共招收学生2000人,其中有300人参与学习先修课程,两年全校共有优等生200人,学习先修课程的优等生有60人.这两年学习先修课程的学生都参加了考试,并且都参加了某高校的自主招生考试(满分100分),结果如下表所示:
分数 |
|
|
|
|
|
人数 | 20 | 55 | 105 | 70 | 50 |
参加自主招生获得通过的概率 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
(1)填写列联表,并画出列联表的等高条形图,并通过图形判断学习先修课程与优等生是否有关系,根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | |||
没有学习大学先修课程 | |||
总计 |
(2)已知今年有150名学生报名学习大学先修课程,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人,求他获得某高校自主招生通过的概率;
②设今年全校参加大学先修课程的学生获得某高校自主招生通过的人数为![]() ,求
,求![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,轿车已成为人们上班代步的一种重要工具.现将某人三年以来每周开车从家到公司的时间之和统计如图所示.
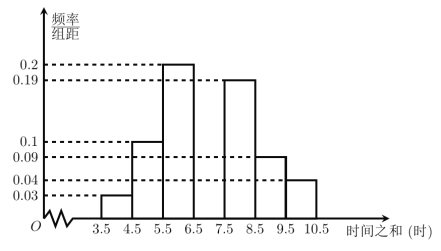
(1)求此人这三年以来每周开车从家到公司的时间之和在![]() (时)内的频率;
(时)内的频率;
(2)求此人这三年以来每周开车从家到公司的时间之和的平均数(每组取该组的中间值作代表);
(3)以频率估计概率,记此人在接下来的四周内每周开车从家到公司的时间之和在![]() (时)内的周数为
(时)内的周数为![]() ,求
,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com