
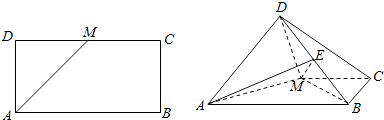
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
(Ⅱ)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
【答案】证明:(Ⅰ)∵长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点, ∴AM=BM=2,∴BM⊥AM.
,M为DC的中点, ∴AM=BM=2,∴BM⊥AM.
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM平面ABCM
∴BM⊥平面ADM
∵AD平面ADM∴AD⊥BM;
(Ⅱ)建立如图所示的直角坐标系,设 ![]() ,
,
则平面AMD的一个法向量 ![]() =(0,1,0),
=(0,1,0), ![]() =
= ![]() +
+ ![]() =(1﹣λ,2λ,1﹣λ),
=(1﹣λ,2λ,1﹣λ), ![]() =(﹣2,0,0),
=(﹣2,0,0),
设平面AME的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则 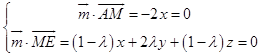 ,
,
取y=1,得x=0,z= ![]() ,
,
则 ![]() =(0,1,
=(0,1, ![]() ),
),
∵cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,∴求得
,∴求得 ![]() ,
,
故E为BD的中点.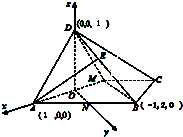
【解析】(Ⅰ)根据线面垂直的性质证明BM⊥平面ADM即可证明AD⊥BM(Ⅱ)建立空间坐标系,求出平面的法向量,利用向量法建立二面角的夹角关系,解方程即可.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
【题目】已知点F为抛物线y 2=﹣8x的焦点,O为原点,点P是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PO|的最小值为( )
A.6
B.![]()
C.![]()
D.4+2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 在
在 ![]() 上有最大值1和最小值0,设
上有最大值1和最小值0,设 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)若不等式 ![]() 在
在 ![]() 上有解,求实数
上有解,求实数 ![]() 的取值范围;
的取值范围;
(3)若方程 ![]() (
( ![]() 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为响应国家节能减排建设的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告: ①80部手机,一年就会增加一吨二氧化氮的排放.
②人们在享受汽车带了的便捷舒适的同时,却不得不呼吸汽车排放的尾气.
活动组织者为了解是市民对这两则广告的宣传效果,随机对10﹣60岁的人群抽查了n人,并就两个问题对选取的市民进行提问,其抽样人数频率分布直方图如图所示,宣传效果调查结果如表所示.
宣传效果调查表
广告一 | 广告二 | |||
回答正 | 占本组 | 回答正 | 占本组 | |
[10,20) | 90 | 0.5 | 45 | a |
[20,30) | 225 | 0.75 | k | 0.8 |
[30,40) | b | 0.9 | 252 | 0.6 |
[40,50) | 160 | c | 120 | d |
[50,60] | 10 | e | f | g |
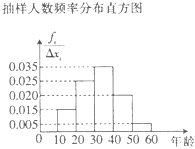
(1)分别写出n,a,b,c,d的值.
(2)若将表中的频率近似看作各年龄组正确回答广告内容的概率,规定正确回答广告一的内容得30元,广告二的内容得60元.组织者随机请一家庭的两成员(大人45岁,孩子17岁),指定大人回答广告一的内容,孩子回答广告二的内容,求该家庭获得奖金数ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
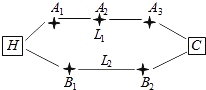
【题目】如图,李先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为 ![]() ;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为 ![]() ,
, ![]() .
. 
(1)若走L1路线,求最多遇到1次红灯的概率;
(2)若走L2路线,求遇到红灯次数X的数学期望;
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com