
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
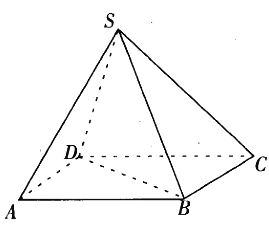
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析;(2)![]()
【解析】试题分析:(Ⅰ)首先利用正弦定理求得![]() ,由此可推出
,由此可推出![]() ,然后利用勾股定理推出
,然后利用勾股定理推出![]() ,从而使问题得证;(Ⅱ)利用等积法将问题转化为
,从而使问题得证;(Ⅱ)利用等积法将问题转化为![]() 求解即可.
求解即可.
试题解析:(Ⅰ)证明:在![]() 中,
中, ![]() ,由已知
,由已知![]() ,
, ![]() ,
, ![]() ,
,
解得![]() ,所以
,所以![]() ,即
,即![]() ,可求得
,可求得![]() .
.
在![]() 中,
中,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)由题意可知, ![]() 平面
平面![]() ,则
,则![]() 到面
到面![]() 的距离等于
的距离等于![]() 到面
到面![]() 的距离,
的距离,
在![]() 中,易求
中,易求![]() ,
,
![]() ,
,
且![]() ,
, ![]() 面
面![]() ,
,
则![]() ,即
,即![]() ,则
,则![]() ,
,
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
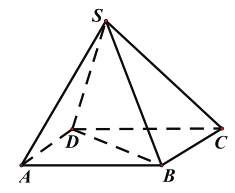
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型,(1)证明线面、面面平行,需转化为证明线线平行;(2)证明线面垂直,需转化为证明线线垂直;(3)证明线线垂直,需转化为证明线面垂直.


科目:高中数学 来源: 题型:
【题目】如图甲,已知矩形![]() 中,
中, ![]() 为
为![]() 上一点,且
上一点,且![]() ,垂足为
,垂足为![]() ,现将矩形
,现将矩形![]() 沿对角线
沿对角线![]() 折起,得到如图乙所示的三棱锥
折起,得到如图乙所示的三棱锥![]() .
.

(Ⅰ)在图乙中,若![]() ,求
,求![]() 的长度;
的长度;
(Ⅱ)当二面角![]() 等于
等于![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前项n和为Sn , 且3Sn=4an﹣4.又数列{bn}满足bn=log2a1+log2a2+…+log2an .
(1)求数列{an}、{bn}的通项公式;
(2)若 ![]() ,求使得不等式
,求使得不等式 ![]() 恒成立的实数k的取值范围.
恒成立的实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() ,
, ![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=
)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min= ![]() ,则φ=( )
,则φ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xm﹣ ![]() ,且f(3)=
,且f(3)= ![]() .
.
(1)求函数f(x)的解析式,并判断函数f(x)的奇偶性.
(2)证明函数f(x)在(0,+∞)上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于x的不等式4x+x﹣a≤ ![]() 在x∈[0,
在x∈[0, ![]() ]上恒成立,则实数a的取值范围是( )
]上恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ![]() ]
]
B.(0,1]
C.[﹣ ![]() ,1]
,1]
D.[1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com