
【题目】为迎接2017年“双![]() ”,“双
”,“双![]() ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共![]() 个,生产一个汤碗需
个,生产一个汤碗需![]() 分钟,生产一个花瓶需
分钟,生产一个花瓶需![]() 分钟,生产一个茶杯需
分钟,生产一个茶杯需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润![]() 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润![]() 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润![]() 元.
元.
(1)使用每天生产的汤碗个数![]() 与花瓶个数
与花瓶个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
【答案】(1)![]() ;(2)
;(2)![]() 元.
元.
【解析】试题分析:(1)由题意可得利润ω=5x+6y+3(100-x-y)=2x+3y+300;(2)根据题意得到约束条件和目标函数,根据线性规划的解题步骤求解即可。
试题解析:
(1)依题意每天生产的茶杯个数为100-x-y,
所以利润ω=5x+6y+3(100-x-y)=2x+3y+300.
(2)由条件得约束条件为
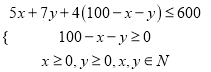 ,即
,即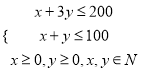 ,
,
目标函数为ω=2x+3y+300,
作出不等式组表示的平面区域(如图所示),
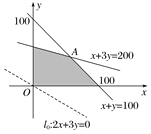
作初始直线l0:2x+3y=0,平移l0,由图形知当l0经过点A时,直线在y轴上的截距最大,此时ω有最大值,
由![]() ,解得
,解得![]()
∴最优解为A(50,50),
∴![]() 元.
元.
故每天生产汤碗50个,花瓶50个,茶杯0个时利润最大,且最大利润为550元.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点. 将
的中点. 将![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图2所示.
,如图2所示.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆
是椭圆![]() :
: ![]() 上的一点,椭圆的右焦点为
上的一点,椭圆的右焦点为![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 三点互不重合.
三点互不重合.
(1)求椭圆![]() 的方程;
的方程;
(2)求证:直线![]() ,
, ![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差大于零的等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是等差数列,且
是等差数列,且![]() ,求非零常数
,求非零常数![]() 的值.
的值.
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,是否存在正整数
项和,是否存在正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a|x+b|(a>0,a≠1,b∈R).
(1)若f(x)为偶函数,求b的值;
(2)若f(x)在区间[2,+∞)上是增函数,试求a、b应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是一个几何体的直观图和三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
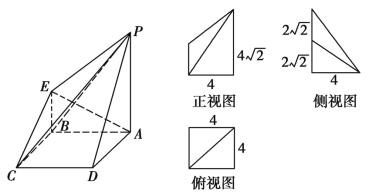
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料![]() ,五合板
,五合板![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料![]() 、五合板
、五合板![]() ;生产每个书橱需要方木枓
;生产每个书橱需要方木枓![]() 、五合板
、五合板![]() .出售一张书桌可获利润
.出售一张书桌可获利润![]() 元,出售一个书橱可获利润
元,出售一个书橱可获利润![]() 元,怎样安排生产可使所得利润最大?最大利润为多少?
元,怎样安排生产可使所得利润最大?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com