
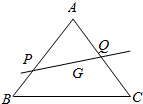
 如图,设G为△ABC的重心,过G的直线l分别交AB,AC于P,Q,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$,$\overrightarrow{AQ}$=n$\overrightarrow{AC}$,令$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$
如图,设G为△ABC的重心,过G的直线l分别交AB,AC于P,Q,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$,$\overrightarrow{AQ}$=n$\overrightarrow{AC}$,令$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$分析 (1)连接AG并延长交BC于点D,则D为BC的中点,则由三角形的重心的性质可得AG=$\frac{2}{3}$AD,$\overrightarrow{AG}$=$\frac{2}{3}$$\overrightarrow{AD}$ 化简可得解雇.
(2)根据$\overrightarrow{AP}$=$\overrightarrow{AG}$+$\overrightarrow{GP}$,可得(1-x)$\overrightarrow{AP}$=$\overrightarrow{AG}$-x•$\overrightarrow{AQ}$.化简可得(m-mx-$\frac{1}{3}$)$\overrightarrow{a}$+(nx-$\frac{1}{3}$)$\overrightarrow{b}$=$\overrightarrow{0}$,可得m-mx-$\frac{1}{3}$=0,且 nx-$\frac{1}{3}$=0,由此证得$\frac{1}{m}$+$\frac{1}{n}$=3.
解答  解:(1)连接AG并延长交BC于点D,则D为BC的中点,则由三角形的重心的性质可得AG=$\frac{2}{3}$AD,
解:(1)连接AG并延长交BC于点D,则D为BC的中点,则由三角形的重心的性质可得AG=$\frac{2}{3}$AD,
∴$\overrightarrow{AG}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$•$\frac{\overrightarrow{a}+\overrightarrow{b}}{2}$=$\frac{1}{3}$($\overrightarrow{a}$+$\overrightarrow{b}$).
(2)∵$\overrightarrow{AP}$=$\overrightarrow{AG}$+$\overrightarrow{GP}$=$\overrightarrow{AG}$+x$\overrightarrow{QP}$=$\overrightarrow{AG}$+x($\overrightarrow{AP}$-$\overrightarrow{AQ}$);
∴(1-x)$\overrightarrow{AP}$=$\overrightarrow{AG}$-x•$\overrightarrow{AQ}$.
又$\overrightarrow{AG}$=$\frac{\overrightarrow{a}+\overrightarrow{b}}{3}$,$\overrightarrow{AP}$=m$\overrightarrow{AB}$,$\overrightarrow{AQ}$=n$\overrightarrow{AC}$,∴(1-x)$\overrightarrow{a}$=$\frac{\overrightarrow{a}+\overrightarrow{b}}{3}$-nx•$\overrightarrow{b}$,
即 (m-mx-$\frac{1}{3}$)$\overrightarrow{a}$+(nx-$\frac{1}{3}$)$\overrightarrow{b}$=$\overrightarrow{0}$,∴m-mx-$\frac{1}{3}$=0,且 nx-$\frac{1}{3}$=0.
求得m-$\frac{m}{3n}$=$\frac{1}{3}$,∴$\frac{1}{m}$+$\frac{1}{n}$=3.
点评 本题主要考查向量加法、减法的几何意义,共线向量基本定理,重心的性质:重心到顶点距离是它到对边中点距离的2倍,以及向量加法的平行四边形法则,向量的加法、减法运算,平面向量基本定理,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-4,4} | B. | {-4,0,4} | C. | {-4,0} | D. | {0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com