
【题目】设函数![]() ,其中
,其中![]() ,
,![]()
(1)若![]() ,且
,且![]() 是
是![]() 的极大值点,求
的极大值点,求![]() 的取值范围;
的取值范围;
(2)当![]() ,
,![]() 时,方程
时,方程![]() 有唯一实数根,求正数
有唯一实数根,求正数![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() ,知
,知![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,故
,故![]() .由此能求出
.由此能求出![]() 的取值范围.
的取值范围.
(2)由方程![]() 有唯一实数解,知
有唯一实数解,知![]() 有唯一实数解,设
有唯一实数解,设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() .由此入手能够推导出正数
.由此入手能够推导出正数![]() 的值.
的值.
解:(1)∵![]() ,其中
,其中![]() ,
,![]()
∴![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() .
.
①若![]() ,由
,由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,所以
单调递减,所以![]() 是
是![]() 的极大值点.
的极大值点.
②若![]() ,则
,则![]() ,得
,得![]() ,或
,或![]() ,∵
,∵![]() 是
是![]() 的极大值点,
的极大值点,
∴![]() ,解得
,解得![]() .
.
综合①②,得![]() 的取值范围是
的取值范围是![]() .
.
(2)∵方程![]() 中唯一实数解,∴
中唯一实数解,∴![]() 有唯一实数解,
有唯一实数解,
设![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() .∵
.∵![]() ,∴
,∴![]() ,
,
方程有两异号根![]() ,设
,设![]() ,∵
,∵![]() ,∴
,∴![]() 应舍去.
应舍去.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,![]() 取最小值
取最小值![]() .
.
∵![]() 有唯一解,∴
有唯一解,∴![]() ,
,
则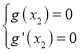 ,即
,即 ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() (*),
(*),
设函数![]() ,∵当
,∵当![]() 时,
时,![]() 是增函数,
是增函数,
∴![]() 至多有一解,∵
至多有一解,∵![]() ,∴方程(*)的解为
,∴方程(*)的解为![]() ,
,
代入方程组解得![]() .
.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
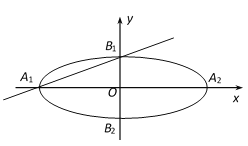
【题目】在平面直角坐标系![]() 中,如图,已知椭圆E:
中,如图,已知椭圆E:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() .设直线
.设直线![]() 倾斜角的余弦值为
倾斜角的余弦值为![]() ,圆
,圆![]() 与以线段
与以线段![]() 为直径的圆关于直线
为直径的圆关于直线![]() 对称.
对称.
(1)求椭圆E的离心率;
(2)判断直线![]() 与圆
与圆![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆![]() 的面积为
的面积为![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设θ∈[0,π],且f(θ)![]() 1,求θ的值;
1,求θ的值;
(2)在△ABC中,AB=1,f(C)![]() 1,且△ABC的面积为
1,且△ABC的面积为![]() ,求sinA+sinB的值.
,求sinA+sinB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x+3|+|2x﹣1|.
(1)求不等式f(x)≤6的解集;
(2)若关于x的不等式f(x)<|m﹣1|的解集非空,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
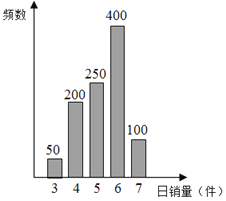
【题目】某公司销售部随机抽取了1000名销售员1天的销售记录,经统计,其柱状图如图.
该公司给出了两种日薪方案.
方案1:没有底薪,每销售一件薪资20元;
方案2:底薪90元,每日前5件的销售量没有奖励,超过5件的部分每件奖励20元.
(1)分别求出两种日薪方案中日工资y(单位:元)与销售件数n的函数关系式;
(2)若将频率视为概率,回答下列问题:
(Ⅰ)根据柱状图,试分别估计两种方案的日薪X(单位:元)的数学期望及方差;
(Ⅱ)如果你要应聘该公司的销售员,结合(Ⅰ)中的数据,根据统计学的思想,分析选择哪种薪资方案比较合适,并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com