
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,解代表空气污染越严重:
| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
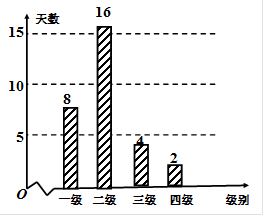
(1)该城市一个月内空气质量类别为良的概率为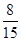 ;
;
(2)至少有一天空气质量类别为中度污染的概率为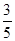 .
.
解析试题分析:(1)由条形图可知空气质量类别为良的天数为16,所以概率为良的概率为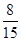 ;
;
(2)从空气质量级别为三级和四级的数据中任取2个,基本事件有15个,其中至少有一天空气质量类别为中度污染的事件有9个,所以概率为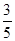 .
.
试题解析:(1)由条形监测图可知,空气质量级别为良的天数为16天,所以此次监测结果中空气质量为良的概率为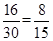 ;
;
(2)样本中空气质量级别为三级的有4天,设其编号为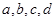 ;样本中空气质量级别为四级的有2天,设其编号为
;样本中空气质量级别为四级的有2天,设其编号为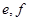 ,则基本事件有:
,则基本事件有: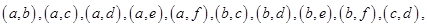
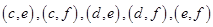 共15个,其中至少有一天空气质量类别为中度污染的情况有:
共15个,其中至少有一天空气质量类别为中度污染的情况有: 共9个,所以至少有一天空气质量类别为中度污染的概率为
共9个,所以至少有一天空气质量类别为中度污染的概率为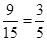 .
.
考点:统计与概率.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是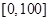 ,样本数据分组为
,样本数据分组为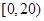 ,
,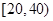 ,
,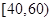 ,
,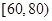 ,
,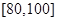 .
.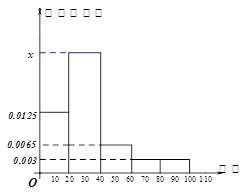
(1)求直方图中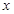 的值;
的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.下面是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图: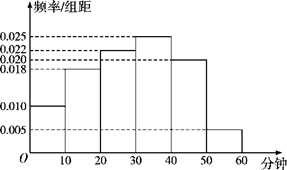
将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?
| | 非积极分子 | 积极分子 | 合计 |
| 男 | | 15 | 45 |
| 女 | | | |
| 合计 | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某电视台为宣传安徽,随机对安徽15~65岁的人群抽取了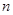 人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示:
人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示:
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
| 第1组 | [15,25) |  | 0.5 |
| 第2组 | [25,35) | 18 |  |
| 第3组 | [35,45) |  | 0.9[ |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65) | 3 |  |

 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如下表l,表2.
表1:男生“智力评分”频数分布表
| 智力评分 | 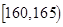 | 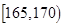 | 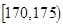 | 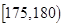 | 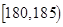 | 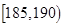 |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 智力评分 | 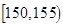 | 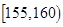 | 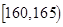 | 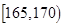 | 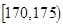 | 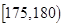 |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为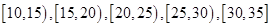 ,得到如题(16)图所示的频率分布直方图。已知生产的产品数量在
,得到如题(16)图所示的频率分布直方图。已知生产的产品数量在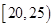 之间的工人有6位.
之间的工人有6位.
(1)求 ;
;
(2)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,求这2位工人不在同一组的概率.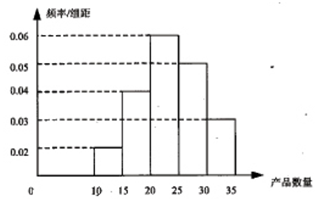
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,决定从本单位全体650人中采用分层抽样的办法抽取50人进行问卷调查,得到了如下列联表:
| | 喜欢户外运动 | 不喜欢户外运动 | 合计 |
| 男性 | | 5 | |
| 女性 | 10 | | |
| 合计 | | | 50 |
 .
. 的把握认为喜欢户外运动与性别有关?并说明你的理由.
的把握认为喜欢户外运动与性别有关?并说明你的理由. | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况,设 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0 16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0 40 |
| 第4组 | [80,90) | ▓ | 0 08 |
| 第5组 | [90,100] | 2 | b |
| | 合计 | ▓ | ▓ |

 的值;
的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com