
【题目】某消费者协会在3月15号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的1000名群众中随机抽取n名群众,按他们的年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,其中第1组
,其中第1组![]() 有6人,得到的频率分布直方图如图所示.
有6人,得到的频率分布直方图如图所示.
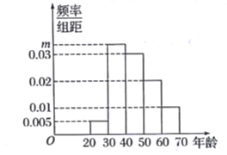
(1)求m,n的值,并估计抽取的n名群众中年龄在![]() 的人数;
的人数;
(2)已知第1组群众中男性有2人,组织方要从第1组中随机抽取3名群众组成维权志愿者服务队,求至少有两名女生的概率.
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】如图,五面体A﹣BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A﹣BC﹣C1为直二面角.
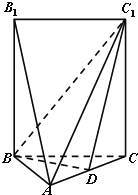
(1)D在AC上运动,当D在何处时,有AB1//平面BDC1,并且说明理由;
(2)当AB1//平面BDC1时,求二面角C﹣BC1﹣D余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,两焦点与短轴的一个端点的连线构成的三角形面积为
,两焦点与短轴的一个端点的连线构成的三角形面积为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设与圆O:![]() 相切的直线l交椭圆C于A,B两点(O为坐标原点),求△AOB面积的最大值。
相切的直线l交椭圆C于A,B两点(O为坐标原点),求△AOB面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德(公元前287年—公元前212年),伟大的古希腊哲学家、数学家和物理学家,他死后的墓碑上刻着一个“圆柱容球”的立体几何图形,为纪念他发现“圆柱内切球的体积是圆柱体积的![]() ,且球的表面积也是圆柱表面积的
,且球的表面积也是圆柱表面积的![]() ”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为
”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为![]() ,则该圆柱的内切球体积为( )
,则该圆柱的内切球体积为( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果,随机在这两种方案中各任意抽取了40件产品作为样本逐件称出它们的重量(单位:克),重量值落在![]() 之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
| 6 | 2 |
| 8 | 12 |
| 14 | 18 |
| 8 | 6 |
| 4 | 2 |
(1)根据上表数据求甲(同组中的重量值用组中点数值代替)方案样本中40件产品的平均数和中位数
(2)由以上统计数据完成下面![]() 列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.814 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com