
【题目】如图所示,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为4的直角三角形.

(1)求该椭圆的离心率和标准方程;
(2)过B1作直线交椭圆于P、Q两点,使PB2⊥QB2,求△PB2Q的面积.
【答案】(1) ![]() +
+![]() =1
=1![]() (2)
(2) ![]()
【解析】试题分析:(Ⅰ)设椭圆的方程为![]() ,F2(c,0),利用△AB1B2是的直角三角形,|AB1|=AB2|,可得∠B1AB2为直角,从而
,F2(c,0),利用△AB1B2是的直角三角形,|AB1|=AB2|,可得∠B1AB2为直角,从而![]() ,利用c2=a2﹣b2,可求
,利用c2=a2﹣b2,可求![]() ,又S=
,又S=![]() |B1B2||OA|=
|B1B2||OA|=![]() =4,故可求椭圆标准方程;
=4,故可求椭圆标准方程;
(Ⅱ)由(Ⅰ)知B1(﹣2,0),B2(2,0),由题意,直线PQ的倾斜角不为0,故可设直线PQ的方程为x=my﹣2,代入椭圆方程,消元可得(m2+5)y2﹣4my﹣16﹣0,利用韦达定理及PB2⊥QB2,利用![]() 可求m的值,进而可求△PB2Q的面积.
可求m的值,进而可求△PB2Q的面积.
解:(Ⅰ)设椭圆的方程为![]() ,F2(c,0)
,F2(c,0)
∵△AB1B2是的直角三角形,|AB1|=AB2|,∴∠B1AB2为直角,从而|OA|=|OB2|,即![]()
∵c2=a2﹣b2,∴a2=5b2,c2=4b2,∴![]()
在△AB1B2中,OA⊥B1B2,∴S=![]() |B1B2||OA|=
|B1B2||OA|=![]()
∵S=4,∴b2=4,∴a2=5b2=20
∴椭圆标准方程为![]() ;
;
(Ⅱ)由(Ⅰ)知B1(﹣2,0),B2(2,0),由题意,直线PQ的倾斜角不为0,故可设直线PQ的方程为x=my﹣2
代入椭圆方程,消元可得(m2+5)y2﹣4my﹣16=0①
设P(x1,y1),Q(x2,y2),
∴![]() ,
,![]()
∵![]() ,
,![]()
∴![]() =
=![]()
∵PB2⊥QB2,∴![]()
∴![]() ,∴m=±2
,∴m=±2
当m=±2时,①可化为9y2±8y﹣16﹣0,
∴|y1﹣y2|=![]() =
=![]()
∴△PB2Q的面积S=![]() |B1B2||y1﹣y2|=
|B1B2||y1﹣y2|=![]() ×4×
×4×![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() =80,
=80, ![]() =20,
=20, ![]() yi=184,
yi=184, ![]() =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,b= 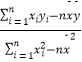 ,a=
,a= ![]() ﹣b
﹣b ![]() ,其中
,其中 ![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个分类变量X和Y,值域分别为{x1,x2}和{y1,y2},其样本频数分别是a=10,b=21,c+d=35.若X与Y有关系的可信程度不小于97.5%,则c等于( )
A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() 是
是![]() 上的一点.
上的一点.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)如图(1),若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(Ⅲ)如图(2),若![]() 是
是![]() 的中点,
的中点,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有两个命题:p:关于x的不等式x2+2x-4-a≥0对一切x∈R恒成立;q:已知a≠0,a≠±1,函数y=-|a|x在R上是减函数,若p∧q为假命题,p∨q为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() (含端点)上运动,当点
(含端点)上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取![]() 名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:

(1)求出表中的![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在![]() 的选取2名担任主要发言人.记这2名主要发言人年龄在
的选取2名担任主要发言人.记这2名主要发言人年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com