
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上成立,求
上成立,求![]() 的取值范围.
的取值范围.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】(本小题10分) 从3名男生和![]() 名女生中任选2人参加比赛。
名女生中任选2人参加比赛。
①求所选2人都是男生的概率;
②求所选2人恰有1名女生的概率;
③求所选2人中至少有1名女生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了![]() 年下半年该市
年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工月工资的中位数为
名农民工月工资的中位数为![]() 百元(假设这
百元(假设这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内)且月工资收入在
(百元)内)且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:

(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名,则能否在犯错误的概率不超过
名,则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1,且E,F分别是BC,B1C1中点.

(1)求证:A1B∥平面AEC1;
(2)求直线AF与平面AEC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在直角坐标系![]() 中,点P到两点
中,点P到两点![]() ,
,![]() 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为![]() ,直线
,直线![]() 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若![]()
![]()
![]() ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|![]() |>|
|>|![]() |.
|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1927年德国汉堡大学的学生考拉兹提出一个猜想:对于每一个正整数,如果它是奇数,就把它乘以3再加1,如果它是偶数,就把它除以2,这样循环,最终结果都能得到1.如图是为了验证考拉兹猜想而设计的一个程序框图,则①处应填写的条件及输出的结果i分别为( )
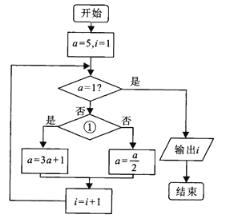
A.a是偶数?;5B.a是偶数?;6
C.a是奇数?;5D.a是奇数?;6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两位运动员每场比赛得分的茎叶图如图所示.
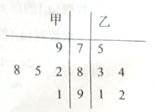
(1)从甲、乙两人的这5次成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;
(2)试用统计学中的平均数、方差知识对甲、乙两位运动员的测试成绩进行分析.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com