
【题目】已知函数,![]() 其中
其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)讨论函数![]() 的单调性及极值;
的单调性及极值;
(Ⅱ)若不等式![]() 在
在![]() 内恒成立,求证:
内恒成立,求证:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)函数求导得![]() ,讨论
,讨论![]() 和
和![]() 演技单调性及极值即可;
演技单调性及极值即可;
(2)当![]() 时,
时,![]() 在
在![]() 内单调递增,可知
内单调递增,可知![]() 在
在![]() 内不恒成立,当
内不恒成立,当![]() 时,
时,![]()
![]() ,即
,即![]() ,所以
,所以![]() .令
.令![]() ,进而通过求导即可得最值.
,进而通过求导即可得最值.
试题解析:
(1)由题意得![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 在
在![]() 内单调递增,没有极值.
内单调递增,没有极值.
当![]() ,即
,即![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
故当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,无极大值.
,无极大值.
综上所述,当![]() 时,
时,![]() 在
在![]() 内单调递增,没有极值;
内单调递增,没有极值;
当![]() 时,
时,![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,
内单调递增,![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
(2)由(1),知当![]() 时,
时,![]() 在
在![]() 内单调递增,
内单调递增,
当![]() 时,
时,![]() 成立.
成立.
当![]() 时,令
时,令![]() 为
为![]() 和
和![]() 中较小的数,
中较小的数,
所以![]() ,且
,且![]() .
.
则![]() ,
,![]() .
.
所以![]() ,
,
与![]() 恒成立矛盾,应舍去.
恒成立矛盾,应舍去.
当![]() 时,
时,![]()
![]() ,
,
即![]() ,
,
所以![]() .
.
令![]() ,
,
则![]() .
.
令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
故![]() 在区间
在区间![]() 内单调递增,
内单调递增,
在区间![]() 内单调递减.
内单调递减.
故![]() ,
,
即当![]() 时,
时,![]() .
.
所以![]() .
.
所以![]() .
.
而![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4tanxsin( ![]() ﹣x)cos(x﹣
﹣x)cos(x﹣ ![]() )﹣
)﹣ ![]() .
.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间[﹣ ![]() ,
, ![]() ]上的单调性.
]上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40﹣t(0≤t≤30且t∈N). 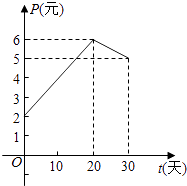
(1)根据提供的图象,求出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)用y(万元)表示该股票日交易额(日交易额=日交易量×每股的交易价格),写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若不等式![]() 对任意
对任意![]() 恒成立.(i)求实数
恒成立.(i)求实数![]() 的取值范围;(ii)试比较
的取值范围;(ii)试比较![]() 与
与![]() 的大小,并给出证明(
的大小,并给出证明(![]() 为自然对数的底数,
为自然对数的底数, ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com