
【题目】空间几何体ABCDEF如图所示.已知面ABCD⊥面ADEF,ABCD为梯形,ADEF为正方形,且AB∥CD,AB⊥AD,CD=4,AB=AD=2,G为CE的中点. (Ⅰ)求证:BG∥面ADEF;
(Ⅱ)求证:面DBG⊥面BDF.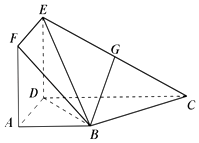
【答案】证明:( I)如图1,取ED中点H,连接HG、AH, 因为G、H分别为EC、ED的中点,所以HG∥CD且 ![]()
因为AB∥CD且 ![]()
所以AB∥HG,且AB=HG.
所以AHGB为平行四边形,所以AH∥BG;
因为BG面PBC,AH面PBC,所以BG∥面ADEF;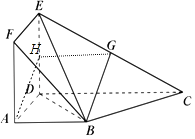
图1
(Ⅱ)如图2,∵ABCD⊥面ADEF及ED⊥DCED⊥面ADCDED⊥DC.
取BD中点O,连接OF,OG、DG
∵AB⊥AD,CD=4,AB=AD=2,∴BF=DF=DB=2 ![]() ,OF⊥BD,OF=
,OF⊥BD,OF= ![]() ,
,
∵BG=AH= ![]() ,DG=
,DG= ![]() EC=
EC= ![]() ,∴OG⊥BD,OG=
,∴OG⊥BD,OG= ![]()
∴∠FOG为二面角F﹣BD﹣G的平面角;
在△OFG中,OF= ![]() ,OG=
,OG= ![]() ,FG=
,FG= ![]() ,
,
满足OF2+OG2=FG2 , ∴∠FOG为直角,
∴面DBG⊥面BDF.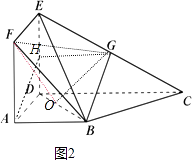
【解析】(Ⅰ)取ED中点H,连接HG、AH,只需证明AH∥BG即可;(Ⅱ)取BD中点O,连接OF,OG、DG,易得∠FOG为二面角F﹣BD﹣G的平面角,解△OFG即可.
【考点精析】通过灵活运用直线与平面平行的判定和平面与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,3,则输出v的值为( ) 
A.20
B.61
C.183
D.548
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为0的等差数列,Sn为数列{an}的前n项和,S5=20,a1 , a3 , a7成等比数列.
(1)求数列{an}的通项公式;
(2)若bn+1=bn+an , 且b1=1,求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系xoy中,点P(1,0),曲线C的参数方程为 ![]() (φ为参数).以原点O为极点,x轴的正半轴为极轴建立极坐标系,倾斜角为α的直线l的极坐标方程为ρsin(α﹣θ)=sinα.
(φ为参数).以原点O为极点,x轴的正半轴为极轴建立极坐标系,倾斜角为α的直线l的极坐标方程为ρsin(α﹣θ)=sinα.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)若曲线C与直线l交于M,N两点,且 ![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,函数
,函数 ![]() ,若函数f(x)图象的两个相邻的对称轴间的距离为
,若函数f(x)图象的两个相邻的对称轴间的距离为 ![]() .
.
(1)求函数f(x)的单调增区间;
(2)在△ABC中,角A,B,C所对的边分别是a,b,c,若△ABC满足f(A)=1,a=3,BC边上的中线长为3,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为D={x|x≠0},且对于任意x1 , x2∈D,有f(x1x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断函数f(x)的奇偶性并证明;
(3)如果f(4)=3,f(x﹣2)+f(x+1)≤3,且f(x)在(0,+∞)上是增函数,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为 ![]() (a>0,β为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程ρcos(θ﹣
(a>0,β为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程ρcos(θ﹣ ![]() )=
)= ![]() .
.
(Ⅰ)若曲线C与l只有一个公共点,求a的值;
(Ⅱ)A,B为曲线C上的两点,且∠AOB= ![]() ,求△OAB的面积最大值.
,求△OAB的面积最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com