（本题满分14分）从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同．
（Ⅰ）若抽取后又放回,抽取3次,求恰好抽到2次为红球的概率;
（Ⅱ）若抽取后不放回,设抽完红球所需的次数为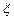
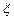,求的分布列及期望．
互动课堂系列答案
激活思维智能训练课时导学练系列答案科目：高中数学 来源： 题型：解答题
某中学在高三开设了4门选修课，每个学生必须且只需选修1门选修课。对于该年级的甲、乙、丙3名学生，回答下面的问题：
（1）求这3名学生选择的选修课互不相同的概率；
（2）某一选修课被这3名学生选修的人数的数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
甲、乙两名篮球运动员互不影响地在同一位置投球，命中率分别为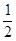
与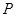
，且乙投球2次均未命中的概率为
。
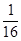（1）求乙投球的命中率。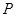
（2）若甲投球1次，乙投球2次，两人共命中的次数记为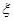
，求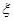的分布列和数学期望。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）某项选拔共有四轮考核，每轮设有一个问题，能正确回答问题者进入下一轮考核，否则即被淘汰．已知某选手能正确回答第一、二、三、四轮的问题的概率分别为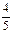
、
、
、
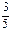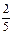，且各轮问题能否正确回答互不影响．
（1）求该选手进入第四轮才被淘汰的概率;
（2）求该选手至多进入第三轮考核的概率． （注：本小题结果可用分数表示）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）在一个选拔项目中，每个选手都需要进行4轮考核，每轮设有一个问题，能正确回答者进入下一轮考核，否则被淘汰。已知某选手能正确回答第一、二、三、四轮问题的概率分别为
、
、
、
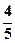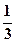，且各轮问题能否正确回答互不影响。
（Ⅰ）求该选手进入第三轮才被淘汰的概率；
（Ⅱ）求该选手至多进入第三轮考核的概率；
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次：“酒后驾车”和“醉酒驾车”，其检测标准是驾驶人员血液中的酒精含量Q（简称血酒含量，单位是毫克/100毫升），当20≤Q≤80时，为酒后驾车；当Q＞80时，为醉酒驾车.济南市公安局交通管理部门于2011年2月的某天晚上8点至11点在市区设点进行一次拦查行动，共依法查出了60名饮酒后违法驾驶机动车者，如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图（其中Q≥140的人数计入120≤Q＜140人数之内）.
（1） 求此次拦查中醉酒驾车的人数；
（2） 从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究，
再从抽取的8人中任取3人，求3人中含有醉酒驾车人数x的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
--------------------------------2分 
-----------4分
-----------------------------------------------------1分
,
,
,
．----------------------------------------------4分 
．--------------------------3分
