
����Ŀ��Ϊ�˽⻧���Ա��������̥ѡ�������Ӱ�죬ij�ش�������Ⱥ�������ȡ������Ϊ![]() �ĵ������������г�����ũ����
�ĵ������������г�����ũ����![]() �ˣ�����
�ˣ�����![]() �ˣ�Ů��
�ˣ�Ů��![]() ��.���Ʋ�ͬȺ��������ѡ��������̥������ѡ��������̥����������ͼ����ͼ��ʾ����������Ӱ���ֱ�ʾ����ѡ��������̥�Ķ�Ӧ�����������������д�����ǣ� ��
��.���Ʋ�ͬȺ��������ѡ��������̥������ѡ��������̥����������ͼ����ͼ��ʾ����������Ӱ���ֱ�ʾ����ѡ��������̥�Ķ�Ӧ�����������������д�����ǣ� ��
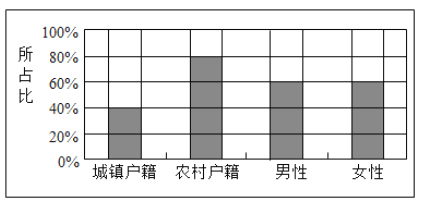
A.�Ƿ�����ѡ��������̥�뻧���й�
B.�Ƿ�����ѡ��������̥���Ա���
C.����ѡ��������̥����Ա�У�����������Ů��������ͬ
D.����ѡ��������̥����Ա�У�ũ�廧���������ڳ�������
���𰸡�C
��������
ͨ���Ķ����⡢ʶͼ�������ݽ��бȶԣ�ͨ������ɵó�Cѡ�����
�ɲ�ͬȺ��������ѡ��������̥������ѡ��������̥����������ͼ֪��
��A�У���������ѡ��������̥�ı���Ϊ![]() ��ũ�廧������ѡ��������̥�ı���Ϊ
��ũ�廧������ѡ��������̥�ı���Ϊ![]() ��
��![]() �Ƿ�����ѡ��������̥�뻧���йأ���A��ȷ��
�Ƿ�����ѡ��������̥�뻧���йأ���A��ȷ��
��B�У���������ѡ��������̥�ı���Ϊ![]() ��Ů������ѡ��������̥�ı���Ϊ
��Ů������ѡ��������̥�ı���Ϊ![]() ��
��
![]() �Ƿ�����ѡ��������̥���Ա��أ���B��ȷ��
�Ƿ�����ѡ��������̥���Ա��أ���B��ȷ��
��C�У���������ѡ��������̥�ı���Ϊ![]() ������Ϊ
������Ϊ![]() �ˣ�
�ˣ�
Ů������ѡ��������̥�ı���Ϊ![]() ������Ϊ
������Ϊ![]() �ˣ�
�ˣ�
![]() ����ѡ��������̥����Ա�У�����������Ů�������࣬��C����
����ѡ��������̥����Ա�У�����������Ů�������࣬��C����
��D�У�����ѡ��������̥����Ա�У�ũ�廧������Ϊ![]() �ˣ���������Ϊ
�ˣ���������Ϊ![]() �ˣ�
�ˣ�
![]() ����ѡ��������̥����Ա�У�ũ�廧���������ڳ�����������D��ȷ��
����ѡ��������̥����Ա�У�ũ�廧���������ڳ�����������D��ȷ��
��ѡ��C��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() ���������
���������![]() ���ܴ���
���ܴ���![]() ��ʹ��
��ʹ��![]() ����ƺ���
����ƺ���![]() ��������
��������![]() ��
��
��1���жϺ���![]() ��
��![]() �Ƿ��������
�Ƿ��������![]() ��˵�����ɣ�
��˵�����ɣ�
��2��������![]() ��
��![]() ��������
��������![]() ����
����![]() ��ֵ��
��ֵ��
��3��������![]() ��
��![]() ����ʵ����
����ʵ����![]() �Ͼ�������
�Ͼ�������![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��a��bΪ�����������������⣺
����a2��b2��1����a��b��1��
����![]() ��1����a��b��1��
��1����a��b��1��
��ea��eb��1����a��b��1��
����lna��lnb��1����a��b��1��
�������������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��alnx+��a+1��x��![]() ��a��0����
��a��0����
��1�����ۺ���f��x���ĵ����ԣ�
��2����f��x���ݩ�![]() +ax+b���������a
+ax+b���������a![]() ʱ��ʵ��b�����ֵ��
ʱ��ʵ��b�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������12�֣�
ijѧУ�������Ƴ�![]() ��
��![]() ��
��![]() ��
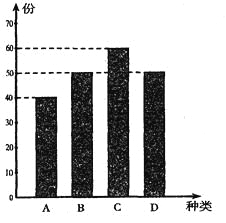
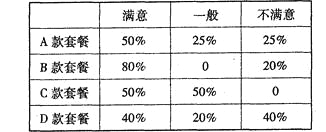
��![]() �Ŀ��ײͣ�ijһ���Ŀ��ײ��������������ͼ����.Ϊ���˽�ͬѧ�����Ƴ����Ŀ��ײ͵����ۣ���ÿλͬѧ���������ʾ����飬Ȼ���÷ֲ�����ķ����ӵ����ʾ��г�ȡ20�ֽ���ͳ�ƣ�ͳ�ƽ�������������ʾ��
�Ŀ��ײͣ�ijһ���Ŀ��ײ��������������ͼ����.Ϊ���˽�ͬѧ�����Ƴ����Ŀ��ײ͵����ۣ���ÿλͬѧ���������ʾ����飬Ȼ���÷ֲ�����ķ����ӵ����ʾ��г�ȡ20�ֽ���ͳ�ƣ�ͳ�ƽ�������������ʾ��
(1) ��ͬѧ��ѡ�����![]() ���ײͣ���ĵ����ʾ���ѡ�еĸ��ʣ�
���ײͣ���ĵ����ʾ���ѡ�еĸ��ʣ�
(2) ����ӵ����ʾ���ѡ������д�������ͬѧ����ѡ��2�˽�����̸������2����������һ��ѡ�����![]() ���ײ͵ĸ��ʡ�
���ײ͵ĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P-ABCD�У�AB//CD����![]() .
.

��1��֤����ƽ��PAB��ƽ��PAD��
��2����PA=PD=AB=DC�� ![]() ��������A-PB-C������ֵ.
��������A-PB-C������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
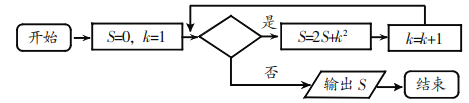
����Ŀ���Ķ���ͼ��ʾ�ij����ͼ�������������Ϊ141�����жϿ���Ӧ���������Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ��������������һ���˵�����߹��ɵ����������Ϊ
��������������һ���˵�����߹��ɵ����������Ϊ![]() .
.
��������ԲC�ķ��̣�
��������ԲO��![]() ���е�ֱ��l����ԲC��A��B���㣨OΪ����ԭ�㣩�����AOB��������ֵ��
���е�ֱ��l����ԲC��A��B���㣨OΪ����ԭ�㣩�����AOB��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��ż����.
��ż����.
��1��������ʽ![]() ������ʵ��
������ʵ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���躯��![]() ����
����![]() ��
��![]() ������㣬��ʵ��
������㣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com