
【题目】已知函数f(x)=|2x﹣1|﹣x,
(1)用分段函数的形式表示该函数,并画出该函数的图象;
(2)写出该函数的值域、单调区间(不要求证明);
(3)若对任意x∈R,不等式|2x﹣1|≥a+x恒成立,求实数a的取值范围.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x
(1)求函数f(x)在R上的解析式;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数中表示同一函数的是( )
①f(x)= ![]() 与g(x)=x
与g(x)=x ![]()
②f(x)=|x|与g(x)= ![]()
③f(x)=x0与g(x)= ![]()
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①③
B.②③
C.③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目, ![]() 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将![]() 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
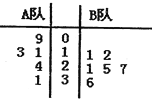
(1)根据茎叶图中的数据,求出![]() 队第六位选手的成绩;
队第六位选手的成绩;
(2)主持人从![]() 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从![]() 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)年产量是多少时,企业所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
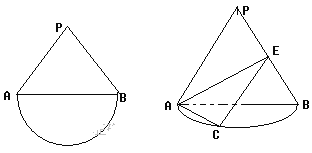
【题目】如图是一个边长为![]() 的正三角形和半圆组成的图形,现把
的正三角形和半圆组成的图形,现把![]() 沿直线AB折起使得与圆所在平面垂直,已知点C是半圆的一个三等分点(靠左边一点),点E是线段PB上的点,(1)当点E是PB的中点时,在圆弧上找一点Q,使得
沿直线AB折起使得与圆所在平面垂直,已知点C是半圆的一个三等分点(靠左边一点),点E是线段PB上的点,(1)当点E是PB的中点时,在圆弧上找一点Q,使得![]() 平面
平面![]() ;(2)当二面角
;(2)当二面角![]() 的正切值为
的正切值为![]() 时,求BE的长。
时,求BE的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
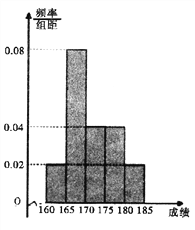
【题目】近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如下图所示:
(I)在第3、4、5组中用分层抽样抽取5名选手,求第3、4、5组每组各抽取多少名选手;
(II)在(I)的前提下,在5名选手中随机抽取2名选手,求第4组至少有一名选手被抽取的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com