已知等比数列{an}中,a2,a3,a4分别是某等差数列的第5项、第3项、第2项,且a1=64,公比q≠1.
(Ⅰ)求an;
(Ⅱ)设bn=log2an,求数列{bn}的前n项和Tn.
解:(Ⅰ)设该等差数列为c
n,则a
2=c
5,a
3=c
3,a
4=c
2∴(a
2-a
3)=2(a
3-a
4)
即:a
1q-a
1q
2=2a
1q
2-2a
1q
3∴

∴
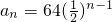
(Ⅱ)

,故b
1=6,d=1
∴

分析:(Ⅰ)由题设条件等比数列{a
n}中,a
2,a
3,a
4分别是某等差数列的第5项、第3项、第2项利用等差数列的性质建立方程,即可求出公比q
(Ⅱ)设b
n=log
2a
n,知数列{b
n}是一个等差数列,其首项与公差易求,利用公式求和即可.
点评:本题考查等差数列与等比数列的综合,考查了用利用等差数列的性质建立方程求参数以及利用等差数列的求和公式求和,考查灵活转化的能力.
