
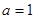 ;⑵
;⑵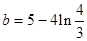 或
或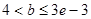 为所求.
为所求. 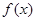 的定义域为
的定义域为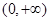
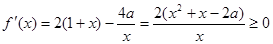
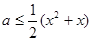 对
对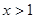 恒成立,记
恒成立,记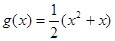
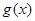 在
在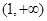 上是增函数,故
上是增函数,故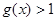 ,所以
,所以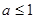
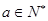 ,所以
,所以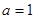 为所求. 5分
为所求. 5分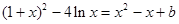 ,整理得
,整理得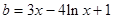
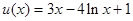 ,则
,则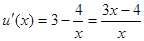
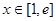 ,故函数
,故函数 在
在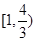 上单调递减,在
上单调递减,在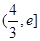 上单调递增.
上单调递增.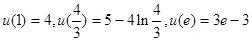 知,
知,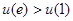
 的方程
的方程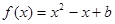 在区间
在区间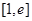 上恰有一个实根 时
上恰有一个实根 时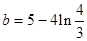 或
或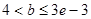 为所求.
为所求. 

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源:不详 题型:解答题
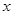 (元/件),可近似看做一次函数
(元/件),可近似看做一次函数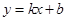 的关系(图象如下图所示).
的关系(图象如下图所示).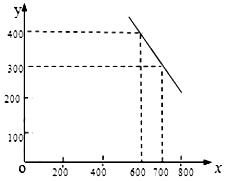
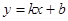 的表达式;
的表达式;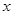 的函数表达式;
的函数表达式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路1的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
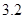 万元、
万元、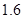 万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) .
万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com