
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建的居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.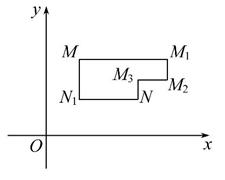
(1)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明).
(2)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度之和最小.
(1)|x-3|+|y-20|,x∈R,y∈[0,+∞)
(2)在点P(3,1)处修建文化中心,可使该文化中心到三个居民区的“L路径”长度之和最小.
解析【解题指南】本题考查了绝对值函数和绝对值不等式的应用.
解:设点P的坐标为(x,y),
(1)点P到居民区A的“L路径”长度最小值为|x-3|+|y-20|,x∈R,y∈[0,+∞).
(2)由题意知,点P到三个居民区的“L路径”长度之和的最小值为点P分别到三个居民区的“L路径”长度最小值之和(记为d)的最小值.
①当y≥1时,d=|x+10|+|x-14|+|x-3|+2|y|+|y-20|,
因为d1(x)=|x+10|+|x-14|+|x-3|≥|x+10|+|x-14|. (*)
当且仅当x=3时,不等式(*)中的等号成立,
又因为|x+10|+|x-14|≥24. (**)
当且仅当x∈[-10,14]时,不等式(**)中的等号成立.
所以d1(x)≥24,当且仅当x=3时,等号成立,
因为d2(y)=2y+|y-20|≥21,当且仅当y=1时,等号成立.故点P的坐标为(3,1)时,P到三个居民区的“L路径”长度之和最小,且最小值为45.
②当0≤y≤1时,由于“L路径”不能进入保护区,所以d=|x+10|+|x-14|+|x-3|+1+|1-y|+|y|+|y-20|.
此时,d1(x)=|x+10|+|x-14|+|x-3|,
d2(y)=1+|1-y|+|y|+|y-20|=22-y≥21.
由①知,d1(x)≥24,故d1(x)+d2(y)≥45,当且仅当x=3,y=1时等号成立.
综上所述,在点P(3,1)处修建文化中心,可使该文化中心到三个居民区的“L路径”长度之和最小.


科目:高中数学 来源: 题型:解答题
如图(1)所示,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器,如图(2)所示,求这个正六棱柱容器容积的最大值.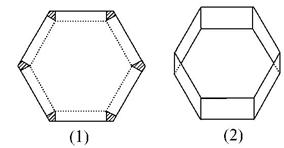
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com