
【题目】已知函数![]() ,如果存在给定的实数对
,如果存在给定的实数对![]() ,使得
,使得![]() 恒成立,则称
恒成立,则称![]() 为“
为“![]() 函数”;
函数”;
(1)判断函数![]() ,
,![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)若![]() 是一个“
是一个“![]() 函数”,求出所有满足条件的有序实数对
函数”,求出所有满足条件的有序实数对![]() ;
;
(3)若定义域为![]() 的函数
的函数![]() 是“
是“![]() 函数”,且存在满足条件的有序实数对
函数”,且存在满足条件的有序实数对![]() 和
和![]() ,当
,当![]() 时,
时,![]() 的值域为
的值域为![]() ,求当
,求当![]() 时
时![]() 的值域;
的值域;
【答案】(1) ![]() 不是“
不是“![]() 函数”, ,
函数”, ,![]() 是“
是“![]() 函数” ;(2)
函数” ;(2)![]() ;(3)
;(3) ![]()
【解析】
(1)分别假设两函数是“![]() 函数”,列出方程恒成立. 通过判断方程的解的个数判断出
函数”,列出方程恒成立. 通过判断方程的解的个数判断出![]() 不是,对于
不是,对于![]() 对于列出方程恒成立,是“
对于列出方程恒成立,是“![]() 函数”.
函数”.
(2)据题中的定义,列出方程恒成立,通过两角和差的正切公式展开整理,令含未知数的系数为0,求出![]() .
.
(3)利用题中的新定义,列出两个等式恒成立;将![]() 用
用![]() 代替,两等式结合得到函数值的递推关系;用不完全归纳的方法求出值域.
代替,两等式结合得到函数值的递推关系;用不完全归纳的方法求出值域.
(1)若![]() 是“
是“![]() 函数”,则存在常数对
函数”,则存在常数对![]() ,使得
,使得![]() .
.
即![]() ,对
,对![]() 恒成立,而
恒成立,而![]() 最多有两个解,
最多有两个解,
所以![]() 不是“
不是“![]() 函数”.
函数”.
若![]() 是
是![]() 函数,则存在常数对
函数,则存在常数对![]() ,使得
,使得![]() ,
,
即存在常数对![]() 满足条件.
满足条件.
所以![]() 是“
是“![]() 函数”.
函数”.
(2) ![]() 是“
是“![]() 函数”,设常数对
函数”,设常数对![]() 满足,
满足,
![]() 恒成立.
恒成立.
当![]() 时,
时,![]() 不是常数.
不是常数.
所以![]() ,
,![]() .
.
![]() .
.
所以![]() 恒成立.
恒成立.
即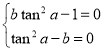 ,即
,即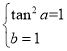 ,所以
,所以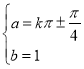 ,
,![]() .
.
又当以![]() ,
,![]() .
.
![]()
所以当![]() 是一个“
是一个“![]() 函数”时,
函数”时,![]() .
.
(3) 函数![]() 是“
是“![]() 函数”,且存在满足条件的有序实数对
函数”,且存在满足条件的有序实数对![]() 和
和![]() .
.
所以![]() ,
, ![]() ,
,
由![]() 得
得![]() .
.
因为![]() 时,
时,![]() 的值域为
的值域为![]() .
.
当![]() 时,
时,![]() ,由
,由![]()
所以![]() 时,
时,![]() 的值域为
的值域为![]() .
.
又![]() 有
有![]() ,即
,即![]() .
.
所以![]() 是以2为周期的函数.
是以2为周期的函数.
当![]() 时
时![]() 的值域为:
的值域为:![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,都有
,都有![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“L函数”.
为“L函数”.
(1)试判断函数![]() 与
与![]() 是否是“L函数”;
是否是“L函数”;
(2)若函数![]() 为“L函数”,求实数a的取值范围;
为“L函数”,求实数a的取值范围;
(3)若函数![]() 为“L函数”,且
为“L函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(﹣1,0)上与函数f(x)的单调性相同的是( )

A.![]() B.y=log2|x|
B.y=log2|x|
C. D.y=cos(2x)
D.y=cos(2x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】纪念币是一个国家为纪念国际或本国的政治、历史,文化等方面的重大事件、杰出人物、名胜古迹、珍稀动植物、体育赛事等而发行的法定货币.我国在1984年首次发行纪念币,目前已发行了115套纪念币,这些纪念币深受邮币爱好者的喜爱与收藏.2019年发行的第115套纪念币“双遗产之泰山币”是目前为止发行的第一套异形币,因为这套纪念币的多种特质,更加受到爱好者追捧.某机构为调查我国公民对纪念币的喜爱态度,随机选了某城市某小区的50位居民调查,调查结果统计如下:
喜爱 | 不喜爱 | 合计 | |
年龄不大于40岁 | 24 | ||
年龄大于40岁 | 20 | ||
合计 | 22 | 50 |
(1)根据已有数据,把表格数据填写完整,判断能否在犯错误的概率不超过![]() 的前提下认为不同年龄与纪念币的喜爱无关?
的前提下认为不同年龄与纪念币的喜爱无关?
(2)已知在被调查的年龄不大于40岁的喜爱者中有5名男性,其中3位是学生,现从这5名男性中随机抽取2人,求至多有1位学生的概率.
附: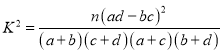 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某省的高考改革方案,考生应在3门理科学科(物理、化学、生物)和3门文科学科(历史、政治、地理)的6门学科中选择3门学科参加考试.根据以往统计资料,1位同学选择生物的概率为0.5,选择物理但不选择生物的概率为0.2,考生选择各门学科是相互独立的.
(1)求1位考生至少选择生物、物理两门学科中的1门的概率;
(2)某校高二段400名学生中,选择生物但不选择物理的人数为140,求1位考生同时选择生物、物理两门学科的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 时,有极值,求
时,有极值,求![]() 的值;
的值;
(2)在直线![]() 上是否存在点
上是否存在点![]() ,使得过点
,使得过点![]() 至少有两条直线与曲线
至少有两条直线与曲线![]() 相切?若存在,求出
相切?若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,动点E到定点![]() 和定直线
和定直线![]() 的距离相等.
的距离相等.
(1)求动点E的轨迹C的方程;
(2)设动直线![]()
![]() 与曲线C有唯一的公共点P,与直线
与曲线C有唯一的公共点P,与直线![]() 相交于点Q,若
相交于点Q,若![]() ,求证:点M的轨迹恒过定点
,求证:点M的轨迹恒过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知曲线![]()
![]() ,曲线
,曲线![]() ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与![]() 都有公共点,则称P为“
都有公共点,则称P为“![]() 型点”.
型点”.
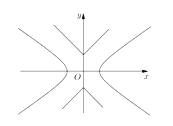
(1)若![]() ,
,![]() 时,判断
时,判断![]() 的左焦点
的左焦点![]() 是否为“
是否为“![]() 型点”,并说明理由;
型点”,并说明理由;
(2)设直线![]() 与
与![]() 有公共点,求证
有公共点,求证![]() ,进而证明原点不是“
,进而证明原点不是“![]() 型点”;
型点”;
(3)若圆![]()
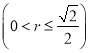 内的任意一点都不是“
内的任意一点都不是“![]() 型点”,试写出a、b满足的关系式,并说明理由.
型点”,试写出a、b满足的关系式,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com