
分析 (1)求导数,f′(x)=(x-2)(x-3),导数为0的实数根为2,3,从而2,3便为f(x)的两极值点,根据p1>p2,便可得出${p}_{1}=\frac{1}{2},{p}_{2}=\frac{1}{3}$;
(2)事件“两人中恰有一人中靶”,包含“甲中靶乙不中靶”和“乙中靶甲不中靶”两个事件,这两个事件显然互斥,从而分别求出这两个事件的概率再求和即可.
解答 解:(1)f′(x)=x2-5x+6=(x-2)(x-3);
∴2,3是f(x)的两个极值点;
p1>p2;
∴$\frac{1}{{p}_{1}}<\frac{1}{{p}_{2}}$;
∴$\frac{1}{{p}_{1}}=2,\frac{1}{{p}_{2}}=3$;
∴${p}_{1}=\frac{1}{2},{p}_{2}=\frac{1}{3}$;
(2)甲中靶乙未中靶的概率为$\frac{1}{2}×(1-\frac{1}{3})=\frac{1}{3}$;
乙中靶甲未中靶的概率为$(1-\frac{1}{2})×\frac{1}{3}=\frac{1}{6}$;
∴两人中恰有一人中靶的概率为$\frac{1}{3}+\frac{1}{6}=\frac{1}{2}$.
点评 考查函数极值点的概念,及极值点的求法,函数在极值点处导数的取值情况,以及独立重复试验的概念,及互斥事件的概率的求法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
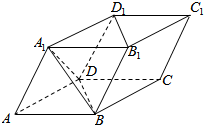 如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).
如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com