
【题目】已知函数f(x)=aln(x+2)﹣x2在(0,1)内任取两个实数p,q,且p>q,若不等式 ![]() 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.(﹣∞,24]
B.(﹣∞,12]
C.[12,+∞)
D.[24,+∞)
【答案】D
【解析】解:根据题意,由 ![]() ,变形可得得f(p+1)﹣f(q+1)>2(p﹣q), 则f(p+1)﹣2(p+1)>f(q+1)﹣2(q+1),
,变形可得得f(p+1)﹣f(q+1)>2(p﹣q), 则f(p+1)﹣2(p+1)>f(q+1)﹣2(q+1),
令g(x)=f(x)﹣2x,则有g(p+1)>r(q+1)
又由实数p、q∈(0,1),且p>q,
所以函数g(x)=f(x)﹣2x在(1,2)上单调递增,
从而 ![]() 在x∈(1,2)上恒成立
在x∈(1,2)上恒成立
即a≥[(x+2)(2x+2)],亦即a≥[(x+2)(2x+2)]max
又函数y=(x+2)(2x+2)=2(x2+3x+2)在x∈[1,2]上单调递增
所以[(x+2)(2x+2)]max=24,
所以a≥24;
故选:D.
【考点精析】解答此题的关键在于理解函数单调性的性质的相关知识,掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集,以及对利用导数研究函数的单调性的理解,了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1﹣ACD外接球的表面积为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为正数,给出下列命题:
①若a2﹣b2=1,则a﹣b<1;
②若 ![]() ﹣
﹣ ![]() =1,则a﹣b<1;
=1,则a﹣b<1;
③ea﹣eb=1,则a﹣b<1;
④若lna﹣lnb=1,则a﹣b<1.
期中真命题的有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,(e为自然对数的底数,a,b∈R),若f(x)在x=0处取得极值,且x﹣ey=0是曲线y=f(x)的切线.
,(e为自然对数的底数,a,b∈R),若f(x)在x=0处取得极值,且x﹣ey=0是曲线y=f(x)的切线.
(1)求a,b的值;
(2)用min{m,n}表示m,n中的最小值,设函数 ![]() ,若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
,若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,M,N分别是AB,PC的中点,若ABCD是平行四边形.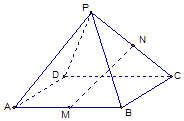
(1)求证:MN∥平面PAD.
(2)若PA=AD=2a,MN与PA所成的角为30°.求MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱.
(1)求该乐队至少演唱1首原创新曲的概率;
(2)假定演唱一首原创新曲观众与乐队的互动指数为a(a为常数),演唱一首经典歌曲观众与乐队的互动指数为2a.求观众与乐队的互动指数之和 ![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com