
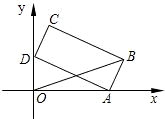
 如图,矩形的长
如图,矩形的长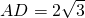 ,宽AB=1,A,D两点分别在x,y轴的正半轴上移动,B,C两点在第一象限.求OB2最大值.
,宽AB=1,A,D两点分别在x,y轴的正半轴上移动,B,C两点在第一象限.求OB2最大值.科目:高中数学 来源: 题型:
 为迎接校庆,学校准备投入a元建造一个花圃(如图).已知矩形ABCD的造价为40元/m2,其余的两个半圆及两个圆的造价为20元/m2.两圆的直径分别为矩形的长和宽,由于矩形ABCD要种名贵花卉,故建造时要求矩形ABCD的面积越大越好.那么,当矩形ABCD的面积达到最大时,
为迎接校庆,学校准备投入a元建造一个花圃(如图).已知矩形ABCD的造价为40元/m2,其余的两个半圆及两个圆的造价为20元/m2.两圆的直径分别为矩形的长和宽,由于矩形ABCD要种名贵花卉,故建造时要求矩形ABCD的面积越大越好.那么,当矩形ABCD的面积达到最大时,| AD | AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
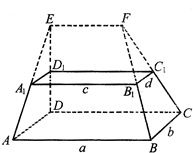 如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h.
如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:
 一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长、宽分别为x、y,剪去部分的面积为20,若2≤x≤10,记y=f(x),则y=f(x)的图象是( )
一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长、宽分别为x、y,剪去部分的面积为20,若2≤x≤10,记y=f(x),则y=f(x)的图象是( )A、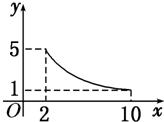 | B、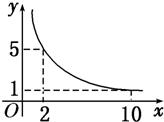 | C、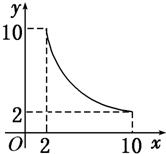 | D、 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com