
【题目】在平面直角坐标系中,点0(0,0),P(6,8),将向量 ![]() 绕点O逆时针方向旋转
绕点O逆时针方向旋转 ![]() 后得向量
后得向量 ![]() ,则点Q的坐标是( )
,则点Q的坐标是( )
A.(﹣7 ![]() ,﹣
,﹣ ![]() )
)
B.(﹣7 ![]() ,
, ![]() )
)
C.(﹣4 ![]() ,﹣2)
,﹣2)
D.(﹣4 ![]() ,2)
,2)
科目:高中数学 来源: 题型:
【题目】某校从参加高三年级期末统考测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.

(Ⅰ)估计这次测试数学成绩的中位数;
(Ⅱ)假设在[90,100]段的学生的数学成绩都不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任意抽取3个数,有放回地抽取了3次,记这3次抽取中,恰好是三个学生的数学成绩的次数为![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中以O为极点,x轴正半轴为极轴建立坐标系.圆C1 , 直线C2的极坐标方程分别为ρ=4sinθ,ρcos( ![]() )=2
)=2 ![]() .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为  (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,(
,(![]() 为坐标原点),直线
为坐标原点),直线![]() :
:![]() .抛物线
.抛物线![]() :
:![]() .
.
(Ⅰ)过直线![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的两条切线,切点为
的两条切线,切点为![]() .求四边形
.求四边形![]() 的面积最小值;
的面积最小值;
(Ⅱ)若圆![]() 过点
过点![]() ,且圆心
,且圆心![]() 在抛物线
在抛物线![]() 上,
上,![]() 是圆
是圆![]() 在
在![]() 轴上截得的弦,试探究
轴上截得的弦,试探究![]() 运动时,弦长
运动时,弦长![]() 是否为定值?并说明理由;
是否为定值?并说明理由;
(Ⅲ) 过点![]() 的直线
的直线![]() 分别与圆
分别与圆![]() 交于点
交于点![]() 两点,若
两点,若![]() ,问直线
,问直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面图形ABB1A1C1C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC= ![]() ,A1B1=A1C1=
,A1B1=A1C1= ![]() .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
(Ⅰ)证明:AA1⊥BC;
(Ⅱ)求AA1的长;
(Ⅲ)求二面角A﹣BC﹣A1的余弦值.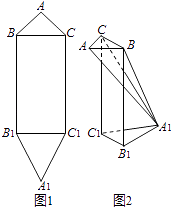
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A、B为抛物线C:![]() 上两点,A与B的中点的横坐标为2,直线AB的斜率为1.
上两点,A与B的中点的横坐标为2,直线AB的斜率为1.
(Ⅰ)求抛物线C的方程;
(Ⅱ)直线![]() 交x轴于点M,交抛物线C:
交x轴于点M,交抛物线C:![]() 于点P,M关于点P的对称点为N,连结ON并延长交C于点H.除H以外,直线MH与C是否有其他公共点?请说明理由.
于点P,M关于点P的对称点为N,连结ON并延长交C于点H.除H以外,直线MH与C是否有其他公共点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
(1)求抛物线准线方程;
(2)若△AOB的面积为4,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.
(1)求x和y的值;
(2)从成绩在90分以上的学生中随机取两名学生,求甲组至少有一名学生的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com