
【题目】已知函数f(x)=lnx+ax在点(t,f(t))处的切线方程为y=3x+1
(1)求a的值;
(2)已知k≤2,当x>1时,f(x)>k(1﹣ ![]() )+2x﹣1恒成立,求实数k的取值范围;
)+2x﹣1恒成立,求实数k的取值范围;
(3)对于在(0,1)中的任意一个常数b,是否存在正数x0 , 使得e ![]() +
+ ![]() x02<1?请说明理由.
x02<1?请说明理由.
【答案】
(1)解:函数f(x)=lnx+ax的导数为f′(x)= ![]() +a,
+a,
在点(t,f(t))处切线方程为y=3x+1,
可得f′(t)= ![]() +a,
+a,
∴函数的切线方程为y﹣(lnt+at)=( ![]() +a)(x﹣t),即y=(
+a)(x﹣t),即y=( ![]() +a)x+lnt﹣1,
+a)x+lnt﹣1,
∴ 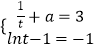 ,
,
解得a=2;
(2)证明:由(1)可得f(x)=lnx+2x,
∵f(x)>k(1﹣ ![]() )+2x﹣1,
)+2x﹣1,
∴lnx>k(1﹣ ![]() )﹣1
)﹣1
即为xlnx+x﹣k(x﹣3)>0,
可令g(x)=xlnx+x﹣k(x﹣3),
g′(x)=2+lnx﹣k,
由x>1,可得lnx>0,2﹣k≥0,
即有g′(x)>0,g(x)在(1,+∞)递增,
可得g(x)>g(1)=1+2k≥0,
∴﹣ ![]() ≤k≤2
≤k≤2
故k的取值范围为[﹣ ![]() ,2];
,2];
(3)解:对于在(0,1)中的任意一个常数b,
假设存在正数x0,使得:e ![]() +
+ ![]() x02<1.
x02<1.
由ef(x0+1)﹣3x0﹣2+ ![]() x02=eln(x0+1)﹣x0+
x02=eln(x0+1)﹣x0+ ![]() x02=(x0+1)e﹣x0+
x02=(x0+1)e﹣x0+ ![]() x02<1成立,
x02<1成立,
从而存在正数x0,使得上式成立,只需上式的最小值小于0即可.
令H(x)=(x+1)e﹣x+ ![]() x2﹣1,H′(x)=e﹣x﹣(x+1)e﹣x+bx=x(b﹣e﹣x),
x2﹣1,H′(x)=e﹣x﹣(x+1)e﹣x+bx=x(b﹣e﹣x),
令H′(x)>0,解得x>﹣lnb,令H′(x)<0,解得0<x<﹣lnb,
则x=﹣lnb为函数H(x)的极小值点,即为最小值点.
故H(x)的最小值为H(﹣lnb)=(﹣lnb+1)elnb+ ![]() ln2b﹣1=
ln2b﹣1= ![]() ln2b﹣blnb+b﹣1,
ln2b﹣blnb+b﹣1,
再令G(x)= ![]() ln2x﹣xlnx+x﹣1,(0<x<1),
ln2x﹣xlnx+x﹣1,(0<x<1),
G′(x)= ![]() (ln2x+2lnx)﹣(1+lnx)+1=ln2x>0,
(ln2x+2lnx)﹣(1+lnx)+1=ln2x>0,
则G(x)在(0,1)递增,可得G(x)<G(1)=0,则H(﹣lnb)<0.
故存在正数x0=﹣lnb,使得e ![]() +
+![]() x02<1.
x02<1.
【解析】(1)求出f(x)的导数,可得切线的斜率和切点,解方程可得a的值;(2)求出f(x)=lnx+x,要证原不等式成立,即证xlnx+x﹣k(x﹣3)>0,可令g(x)=xlnx+x﹣k(x﹣3),求出导数,判断符号,可得单调性,即可得证;(3)对于在(0,1)中的任意一个常数b,假设存在正数x0 , 使得e ![]() +
+ ![]() x02<1.运用转化思想可令H(x)=(x+1)e﹣x+
x02<1.运用转化思想可令H(x)=(x+1)e﹣x+ ![]() x2﹣1,求出导数判断单调性,可得最小值,即可得到结论
x2﹣1,求出导数判断单调性,可得最小值,即可得到结论


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线M: ![]() =1(a>0,b>0)的上焦点为F,上顶点为A,B为虚轴的端点,离心率e=
=1(a>0,b>0)的上焦点为F,上顶点为A,B为虚轴的端点,离心率e= ![]() ,且S△ABF=1﹣
,且S△ABF=1﹣ ![]() .抛物线N的顶点在坐标原点,焦点为F.
.抛物线N的顶点在坐标原点,焦点为F.
(1)求双曲线M和抛物线N的方程;
(2)设动直线l与抛物线N相切于点P,与抛物线的准线相交于点Q,则以PQ为直径的圆是否恒过y轴上的一个定点?如果经过,试求出该点的坐标,如果不经过,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y= ![]() x2的图象在点(x0 ,
x2的图象在点(x0 , ![]() x02)处的切线为l,若l也为函数y=lnx(0<x<1)的图象的切线,则x0必须满足( )
x02)处的切线为l,若l也为函数y=lnx(0<x<1)的图象的切线,则x0必须满足( )
A.![]() <x0<1
<x0<1
B.1<x0< ![]()
C.![]() <x0<
<x0< ![]()
D.![]() <x0<2
<x0<2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() 满足
满足![]() ,
, ![]() ,
, ![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求和: ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据等差数列![]() 的
的![]() ,
, ![]() ,列出关于首项
,列出关于首项![]() 、公差
、公差![]() 的方程组,解方程组可得
的方程组,解方程组可得![]() 与
与![]() 的值,从而可得数列
的值,从而可得数列![]() 的通项公式;(2)利用已知条件根据题意列出关于首项
的通项公式;(2)利用已知条件根据题意列出关于首项![]() ,公比
,公比![]() 的方程组,解得
的方程组,解得![]() 、
、![]() 的值,求出数列
的值,求出数列![]() 的通项公式,然后利用等比数列求和公式求解即可.
的通项公式,然后利用等比数列求和公式求解即可.
试题解析:(1)设等差数列{an}的公差为d. 因为a2+a4=10,所以2a1+4d=10.解得d=2.
所以an=2n1.
(2)设等比数列的公比为q. 因为b2b4=a5,所以b1qb1q3=9.
解得q2=3.所以![]() .
.
从而![]() .
.
【题型】解答题
【结束】
18
【题目】已知命题![]() :实数
:实数![]() 满足
满足![]() ,其中
,其中![]() ;命题
;命题![]() :方程
:方程![]() 表示双曲线.
表示双曲线.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某射击运动员,每次击中目标的概率都是0.8.现采用随机模拟的方法估计该运动员射击4次至少击中3次的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了如下20组随机数:
5727 0293 7140 9857 0347
4373 8636 9647 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 6710 4281
据此估计,该射击运动员射击4次至少击中3次的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的4个图像中,与所给3个事件最吻合的顺序为
①我离开家后,心情愉快,缓慢行进,但最后发现快迟到时,加速前进;
②我骑着自行车上学,但中途车坏了,我修理好又以原来的速度前进;
③我快速的骑着自行车,最后发现时间充足,又减缓了速度.

① ② ③ ④
A. ③①② B. ③④② C. ②①③ D. ②④③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com