
【题目】如图是一座桥的截面图,桥的路面由三段曲线构成,曲线AB和曲线DE分别是顶点在路面A、E的抛物线的一部分,曲线BCD是圆弧,已知它们在接点B、D处的切线相同,若桥的最高点C到水平面的距离H=6米,圆弧的弓高h=1米,圆弧所对的弦长BD=10米. 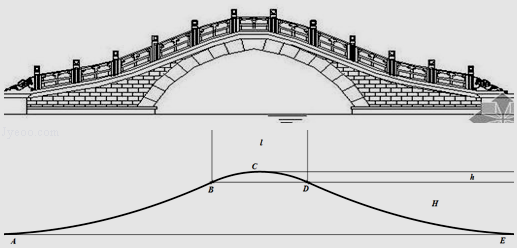
(1)求弧 ![]() 所在圆的半径;
所在圆的半径;
(2)求桥底AE的长.
【答案】
(1)解:设弧 ![]() 所在圆的半径为r(r>0),由题意得r2=52+(r﹣1)2,则r=13,
所在圆的半径为r(r>0),由题意得r2=52+(r﹣1)2,则r=13,
即弧 ![]() 所在圆的半径为13米
所在圆的半径为13米
(2)解:以线段AE所在直线为x轴,线段AE的中垂线为y轴,建立如图的平面直角坐标系.∵H=6米,BD=10米,弓高h=1米,
∴B(﹣5,5),D(5,5),C(0,6),设 ![]() 所在圆的方程为x2+(y﹣b)2=r2,(r>0),
所在圆的方程为x2+(y﹣b)2=r2,(r>0),
则 ![]() ,
, ![]() ,
,
∴弧 ![]() 的方程为x2+(y+7)2=169(5≤y≤6)
的方程为x2+(y+7)2=169(5≤y≤6)
设曲线AB所在抛物线的方程为:y=a(x﹣m)2
由点B(﹣5,5),在曲线AB上
∴5=a(5+m)2,
又弧 ![]() 与曲线段AB在接点B处的切线相同,且弧
与曲线段AB在接点B处的切线相同,且弧 ![]() 在点B处的切线的斜率为
在点B处的切线的斜率为 ![]() ,
,
由y=a(x﹣m)2,y′=2a(x﹣m),2a(﹣5﹣m)= ![]() ,
,
2a(5+m)=﹣ ![]() ,
,
由得m=﹣29,A(﹣29,0),E(29,0)
∴桥底AE的长为58米
【解析】(1)由r2=52+(r﹣1)2 , 即可求得r,即可求得弧 ![]() 所在圆的半径;(2)建立直角坐标系,由题意设
所在圆的半径;(2)建立直角坐标系,由题意设 ![]() 所在圆的方程,列方程组,即可求得圆的方程,曲线AB所在抛物线的方程为:y=a(x﹣m)2 , 求导,根据导数的几何意义,即可求得m的值,求得A和E点坐标,即可求得桥底AE的长为58米.
所在圆的方程,列方程组,即可求得圆的方程,曲线AB所在抛物线的方程为:y=a(x﹣m)2 , 求导,根据导数的几何意义,即可求得m的值,求得A和E点坐标,即可求得桥底AE的长为58米.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据,
(吨标准煤)的几组对照数据,

(1)求![]() ,
, ![]() ,
,
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技动前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
已知![]() ,
, ![]() .
.
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若a2+c2+ ![]() ac=b2 , sinA=
ac=b2 , sinA= ![]() .
.
(1)求sinC的值;
(2)若a=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨1937年提出一个著名的猜想:任给一个正整数 ![]() ,如果
,如果 ![]() 是偶数,就将它减半(即
是偶数,就将它减半(即 ![]() );如果
);如果 ![]() 是奇数,则将它乘3加1(即
是奇数,则将它乘3加1(即 ![]() ),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明。也不能否定,现在请你研究:如果对正整数
),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明。也不能否定,现在请你研究:如果对正整数 ![]() (首项)按照上述规则旅行变换后的第9项为1(注:1可以多次出现),则
(首项)按照上述规则旅行变换后的第9项为1(注:1可以多次出现),则 ![]() 的所有不同值的个数为 .
的所有不同值的个数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项不为零的数列{an}的前n项和为Sn , 且a1=1,Sn=panan+1(n∈N*),p∈R.
(1)若a1 , a2 , a3成等比数列,求实数p的值;
(2)若a1 , a2 , a3成等差数列,
①求数列{an}的通项公式;
②在an与an+1间插入n个正数,共同组成公比为qn的等比数列,若不等式(qn)(n+1)(n+a)≤e对任意的n∈N*恒成立,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分),以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界线符合函数y=x+ ![]() (x>0)模型,园区服务中心P在x轴正半轴上,PO=
(x>0)模型,园区服务中心P在x轴正半轴上,PO= ![]() 百米.
百米. 
(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道PQ最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={x||x|<1},N={y|y=2x , x∈M},则集合R(M∩N)等于( )
A.(﹣∞, ![]() ]
]
B.( ![]() ,1)
,1)
C.(﹣∞, ![]() ]∪[1,+∞)
]∪[1,+∞)
D.[1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com