已知函数f(x)=ex+tx(e为自然对数的底数).
(Ⅰ)当t=-e时,求函数f(x)的单调区间;
(Ⅱ)设不等式f(x)>0的解集为P,且集合{x|0<x≤2}⊆P,求实数t的取值范围.
解:(Ⅰ)当t=-e时,f(x)=e
x-ex,f'(x)=e
x-e.
由f'(x)=e
x-e>0,解得x>1;f'(x)=e
x-e<0,解得x<1.
∴函数f(x)的单调递增区间是(1,+∞);单调递减区间是(-∞,1).
(Ⅱ)由不等式f(x)>0的解集为P,且{x|0<x≤2}⊆P,可知,对于任意x∈(0,2],不等式f(x)>0恒成立,即e
x+tx>0即

在x∈(0,2]上恒成立.
令
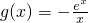
,∴
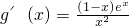
.
当0<x<1时,g'(x)>0;当1<x<2时,g'(x)<0.
∴函数g(x)在(0,1)上单调递增;在(1,2)上单调递减.
∴函数g(x)在x=1处取得极大值g(1)=-e,即为在x∈(0,2]上的最大值.
∴实数t的取值范围是(-e,+∞).
分析:(Ⅰ)求导函数,利用导数的正负,可得函数的单调区间;
(Ⅱ)由不等式f(x)>0的解集为P,且{x|0<x≤2}⊆P,可知对于任意x∈(0,2],不等式f(x)>0恒成立,利用分离参数法,可得

在x∈(0,2]上恒成立,求出右边对应函数的最大值,即可求实数t的取值范围.
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,解题的关键是将问题转化为

在x∈(0,2]上恒成立,利用求出右边对应函数的最大值,可求实数t的取值范围.

 在x∈(0,2]上恒成立.
在x∈(0,2]上恒成立. 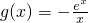 ,∴
,∴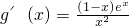 .
. 在x∈(0,2]上恒成立,求出右边对应函数的最大值,即可求实数t的取值范围.
在x∈(0,2]上恒成立,求出右边对应函数的最大值,即可求实数t的取值范围. 在x∈(0,2]上恒成立,利用求出右边对应函数的最大值,可求实数t的取值范围.
在x∈(0,2]上恒成立,利用求出右边对应函数的最大值,可求实数t的取值范围. 

 名校课堂系列答案
名校课堂系列答案